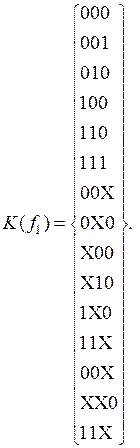Будем полагать, что каждый набор n аргументов ПФ задает вершину n-мерного куба и называется 0-кубом. Определив множество 0-кубов, на которых значения функции равны единице, можно получить представление ПФ в виде кубического комплекса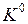 
. Рассмотрим функцию, заданную табл. 3.7. Она может быть представлена в виде следующего кубического комплекса:
,
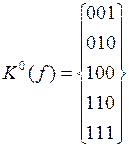где столбцам соответствуют переменные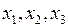 
.
Из способа построения кубического комплекса 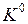следует, что каждая ПФ может иметь единственное представление такого вида.
Для ПФ, в общем случае зависящей от n аргументов, могут быть построены кубические комплексы размерности: ,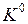 
, 
,…, 
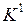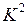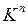. При этом каждый комплекс 
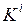строится по комплексу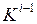 
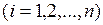путем образования i-кубов из 
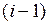-кубов, отличающихся только по одной переменной. Переменная (координата), по которой отличаются сравниваемые кубы, называется независимой и заменяется символом «Х».
В качестве примера рассмотрим функцию
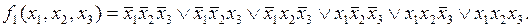
Для нее кубические комплексы 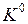, , 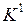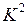и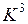 
могут быть построены следующим образом:
; 
; 
.
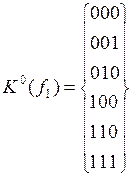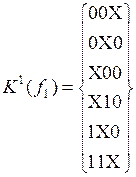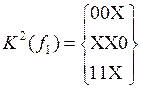Поскольку кубический комплекс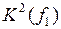 
не содержит 2-кубов, отличающихся только по одной переменной, то кубический комплекс 
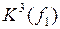будет представлен пустым множеством.
Объединение кубов комплексов 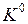, , 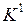,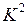…, 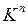образует кубический комплекс 
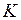. Таким образом,
.
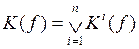Для рассмотренной выше функции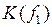 
можно записать в следующем виде:
