В дискретном виде линейные преобразования могут быть описаны в общем виде как векторно-матричные операции [3,5, 16]:
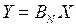(5.11)
где X - вектор отсчетов исходных данных, полученный в результате дискретизации непрерывного сигнала согласно теореме Котельникова, Y - вектор отсчетов результата, BN - матрица размера N´N, определяющая ядро выполняемого преобразования.
К числу подобных преобразований относится циклическая свертка последовательностей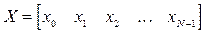 
и 
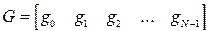, в этом случае строится матрица ядра свертки:
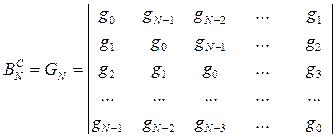
Каждый элемент вектора Y может быть описан как:
; 
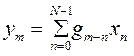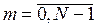. (5.12)
Матрица ядра циклической взаимокорреляции может быть построена как транспонированная матрица ядра свертки, т.е. следующим образом:
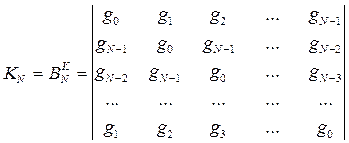
Поэтому каждый отсчет результата может быть записан как:
; 
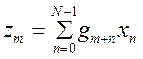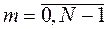(5.13)
причем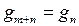 
для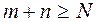 
.
