1.1 В основе построения АЦП лежит дискретизация непрерывного сигнала U(t), представляющая собой измерительное преобразование этого сигнала в последовательность его мгновенных значений Uд(кТу), соответствующих определенным моментам времени (кТц). В данном случае к принадлежит множеству к={1, 2, 3…N}, а Тц – шаг дискретизации. В общем случае взаимосвязь аналоговых и дискретных значений описывается следующей зависимостью
Uд(кТц)=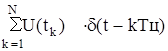 
,
где U( 
) – значение сигнала в момент времени , отмеченного выше множества;
- функция Дирака.
1.2 Дискретизация сигнала по времени выполняется либо с постоянным шагом Тц=const, либо с переменным шагом Тц=var. Независимо от принятого шага дискретизации в дискретном сигнале отсутствуют промежуточные значения между моментами , 
, поэтому в данном преобразовании необходимо восстановить все промежуточные значения с заданной погрешностью. В качестве восстанавливающего сигнала используются различные базисные функции с минимальной средней квадратической погрешностью.
1.3 По принципу действия АЦП делятся на последовательные, параллельные и последовательно-параллельные. При этом последовательную процедуру можно реализовать как развертывающего или следящего уравновешивания, так и последовательных приближений (поразрядного уравновешивания).
В данном макете использован АЦП с последовательным приближением.
Основной характеристикой АЦП является его передаточная характеристика N= f(Uвх).
