Цепи нижних частот второго порядка описываются следующей передаточной функцией
,
где 
полюсы этой функции, 
.
Число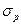 
представляет собой вещественную часть полюсов.
Размещение полюсов 
и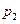 
( 
, 
) на комплексной плоскости, АЧХ 
и ФЧХ 
фильтра нижних частот второго прядка представлены на рис. 2.5.
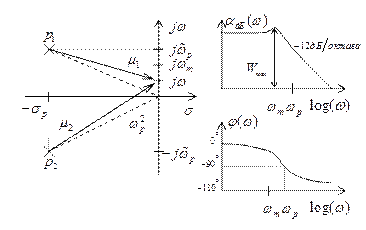
Рис. 2.5 – Фильтр нижних частот второго порядка
Амплитудно-частотная характеристика фильтра, на частоте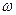 
, определяется следующим выражением
,
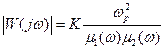или
,
Найдем значение переменной 
, при котором функция 
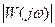принимает наибольшее значение. Так как числитель функции 
это постоянная величина, то функция принимает наибольшее значение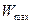 
, при знаменателе функции 
, принимающем наименьшее значение.
Подставим выражения в знаменатель
.
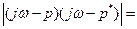
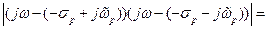
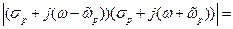
Функция, расположенная под корнем, это неотрицательная и немонотонная функция, имеющая перегибы. Раскроем скобки в этой функции и получим удобное, для нахождения производной, выражение
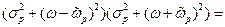
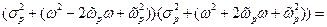
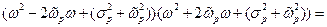
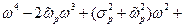
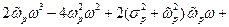
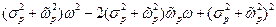
Упростим полученное выражение, группируя коэффициенты при переменных 
, 
, 
,
.
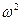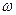
Найдем производную (по переменной 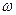) для этого выражение и приравняем производную нулю. Получим следующие уравнение
.
Решение этого уравнения даст точки перегиба. Уравнение станет равенством в двух следующих случаях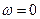: при 
и при 
.
Обозначим переменную 
как искомую переменную 
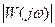. При функция примет наибольшее значение 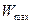. Очевидно, что 
.
Подставим выражение 
в 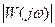и получим выражение для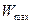
.
Следует отметить, что при 
, а при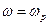 
.
