Комбинационная схема с m выходами описывается системой m логических уравнений. (Для каждого выхода – свое уравнение.)
Простейший подход к синтезу таких схем – реализация каждого уравнения системы в отдельности, но получаемый результат будет далеко не лучшим. При решении задачи оптимального синтеза многовыходных схем возникает много трудностей, не преодоленных до сегодняшнего дня. Существует несколько, достаточно общих, методов синтеза многовыходных комбинационных схем. В основе всех этих методов лежит идея использования одной функции или ее части для получения других функций. Например, пусть заданы функции:

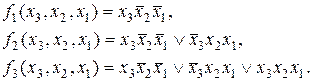
Вполне очевидно, что при синтезе можно использовать соотношения:

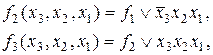
что значительно сократит объем необходимого оборудования.
Удобным и наглядным для синтеза многовыходных схем является способ с использованием карт Карно.
Применение этою способа покажем на примере.
Пусть даны три функции:
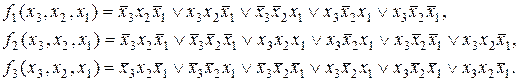
Составим для этих функций карты Карно (табл. 8).
При сравнении карт легко видеть, что функции имеют четыре общих терма (эти термы отмечены звездочкой), которые можно выразить некоторой функцией
 .
.
Таблица 8
| f1
|
|
| f2
|
|
| f3
|
| x3\x2x1
|
|
|
|
|
|
| x3\x2x1
|
|
|
|
|
|
| x3\x2x1
|
|
|
|
|
|
|
|
|
| 1*
|
|
|
|
|
|
| 1*
|
|
|
|
|
|
| 1*
|
|
| 1*
| 1*
|
| 1*
|
|
|
| 1*
| 1*
|
| 1*
|
|
|
| 1*
| 1*
|
| 1*
|
С учетом этого выражения функции f1, f2, f3 можно представить следующим образом
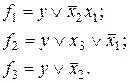
Теперь эти функции можно реализовать обычным образом (не забыв реализовать функцию y).