Число степеней свободы определяет то количество сведений, которое остаётся свободным после использования всей совокупности сведений для определения некоторой статистической характеристики.
Фиксирование объёма выборки и суммирование её значений накладывает на совокупность сведений одну линейную связь (всегда можно вычислить любое значение выборки, если другие значения известны и известно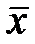 
). Значит число степеней свободы ν=n-1.
В биномиальном распределении и в распределении Пуассона учитываются 2 связи: одна связь, которая возникает при суммировании частот, вторая – связь, которая образуется при определении теоретических параметров распределения (р – при биномиальном и а для распределения Пуассона). Здесь число степеней свободы ν=n-2. При нормальном распределении ν=n-3, т.к.число параметров нормального распределения равно двум (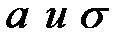 
).
