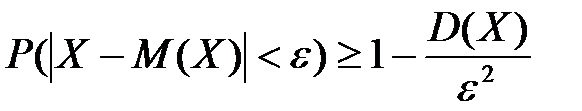ЗБЧ устанавливает устойчивость средних значений: при большом количестве испытаний их средний результат перестаёт быть случайным и может быть предсказан с большой степенью точности.
ЗБЧ представляет ряд математических теорем, в каждой из которых для определённых условий устанавливается факт приближения средних характеристик большого числа испытаний к определённым постоянным. Теоремы ЗБЧ показывают связь между абстрактными теоремами теории вероятностей и опытом и дают возможность предсказать результаты опытов.
Мы уже говорили о теореме Я. Бернулли: при большом числе опытов относительная частота появления события сходится по вероятности к вероятности этого события. Рассмотрим некоторые более общие формы закона больших чисел.
Неравенство Чебышева.
Пусть дана СВ Х с математическим ожиданием М(Х) и дисперсией D(X). Как бы ни мало было постоянное положительное число ɛ, вероятность того, что величина Х отклонится от своего математического ожидания не менее чем на ɛ, ограничена сверху величиной 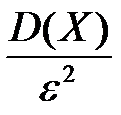 :
: 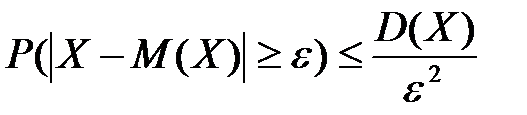 или
или