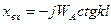
для симметричного вибратора, как правило 
, тогда
Рассмотрим полуволновой вибратор (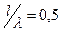 
).
Расчет ведут следующим образом. В вибраторе существуют потери, пусть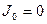 
, тогда 
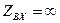, но этого не может быть, так как 
в точке питания он конечен, значит и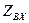 
– конечно.
Закон синуса тока – справедлив для линии без потерь, а у нас существуют потери, значит закон не синусоидальный, а такой, какой бывает в линиях с потерями. Он соответствует закону гиперболического синуса:
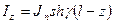
где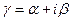 
, 
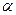– коэффициент затухания и 
– коэффициент фазы.
Поэтому при расчете 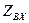«коротких» вибраторов ( 
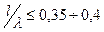и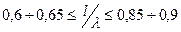 
), то есть у которых узел тока находится от точек питания вибратора не ближе 
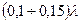, исходят из синусоидального распределения тока.
При расчете 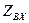«длинных» вибраторов ( 
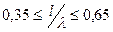) следует исходить из распределения тока по закону 
.
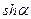Найдем формулу для расчета активной составляющей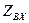
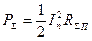через ток в пучности
через ток в точках запитки
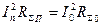
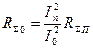
Используя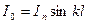 
, получим
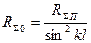
Значение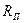 
для данной длины находят из таблиц или графиков
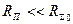для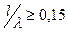 
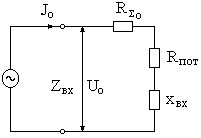
При расчете 
пользуются формулой входного сопротивления разомкнутой на конце двухпроводной линии без потерь, заменяя в ней волновое сопротивление линии волновым сопротивлением антенны (симметричного вибратора)
