Ответим на вопрос об изменении уравнения квадрики при аффинной замене координат x=h+Ty. Положим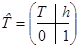 
, тогда равенство x=h+Ty эквивалентно равенству 
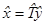, и, значит, 
. Тем самым установлена теорема.
Теорема 5.2. Пусть из квадрики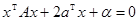 
аффинной заменой координат x=h+Ty получается квадрика 
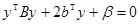, тогда 
, 
, 
, 
.
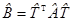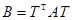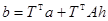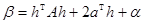Обозначим через s(A) положительный индекс инерции, а через t(A) – отрицательный индекс инерции квадратичной формы. Из приведенных формул вытекает полезное следствие.
Следствие 5.1. Пусть из квадрики 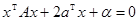аффинной заменой координат получена квадрика 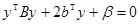. Тогда 
, 
, 
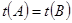и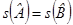 
, 
, 
.
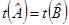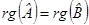Доказательство вытекает из закона инерции квадратичных форм и формул изменения квадрики при аффинной замене системы координат.
Следствие 5.2. Величины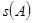 
, 
, 
, 
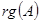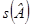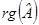являются аффинными инвариантами квадрики.
