Определение 1.Зависимость переменной  от переменной
от переменной 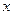 называется функцией, если каждому значению
называется функцией, если каждому значению 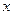 соответствует единственное значение
соответствует единственное значение  .
.
Пишем: 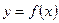 и говорим, что
и говорим, что  есть функция от
есть функция от 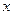 . При этом
. При этом 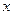 называется независимой переменной (или аргументом), а
называется независимой переменной (или аргументом), а  – зависимой переменной.
– зависимой переменной.
Определение 2. Область определения функции 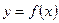 (обозначаемая через
(обозначаемая через 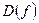 ) – это все значения, которые принимает
) – это все значения, которые принимает 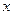 . Множество значений функции (обозначаемое через
. Множество значений функции (обозначаемое через 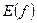 ) – это все значения, которые принимает
) – это все значения, которые принимает  .
.
Определение 3. Функция 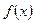 называется возрастающей (убывающей) на числовом промежутке
называется возрастающей (убывающей) на числовом промежутке  , если для любых
, если для любых 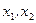 из
из  , таких, что
, таких, что 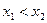 , выполнено неравенство:
, выполнено неравенство:

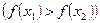 .
.
Определение 4. Функция 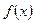 называется монотонной на промежутке
называется монотонной на промежутке  , если она только убывает или только возрастает на
, если она только убывает или только возрастает на  .
.
Определение 5. Функция 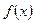 называется четной (нечетной), если её
называется четной (нечетной), если её 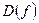 симметрична относительно нуля и для любого
симметрична относительно нуля и для любого  из
из 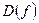 :
:
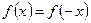
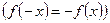 .
.
(Заметим, что 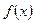 может не являться ни четной, ни нечетной).
может не являться ни четной, ни нечетной).
Определение 6. Функция 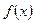 называется периодической, если существует число
называется периодической, если существует число 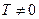 , такое, что для любого
, такое, что для любого 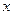 из
из 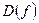 точки
точки 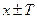 также принадлежат
также принадлежат 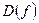 и
и 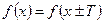 . Наименьшее положительное из таких чисел
. Наименьшее положительное из таких чисел 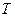 называется периодом функции.
называется периодом функции.