1. Коммутативные законы
А Ù В º В Ù А
А Ú В º В Ú А
2. Ассоциативные законы
А Ù (В Ù С) º (А Ù В)Ù С
А Ú (В Ú С) º (А Ú В)Ú С
3. Дистрибутивные законы
А Ù (В Ú С) º (А Ù В)Ú (А Ù С)
А Ú (В Ù С) º (А Ú В)Ù (А Ú С)
4. А Ù А º А
А Ú А º А
5. А Ù Иº А
А ÚИº И
6. А Ù Лº Л
А ÚЛº А
7. А Ù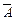 
º Л
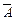А Ú º И
8. 
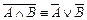
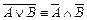
9. 
10. А Þ В º 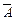Ú В
11. А Þ В º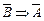 
Докажем равенство 10: А Þ В º 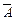Ú В. Для этого составим таблицу истинности.
| А
| В
| А Þ В
|
| 
|
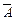
| И
| И
| И
| Л
| И
|
| И
| Л
| Л
| Л
| Л
|
| Л
| И
| И
| И
| И
|
| Л
| Л
| И
| И
| И
|
Т.к. формулы принимают одинаковые значения истинности при всех наборах значений истинности переменных, то они тождественно равны.
Аналогично с помощью таблиц истинности доказываются остальные законы.
С помощью таблиц истинности и законов алгебры высказываний можно доказать равносильность составных формул высказываний (смотри рекомендации по решению задач).
Контрольные вопросы
1. Какие предложения называются высказываниями?
2. Какие высказывания называют элементарными, а какие – составными?
3. Сформулируйте определения отрицания, конъюнкции, дизъюнкции, импликации, эквиваленции высказываний и составьте для данных операций над высказываниями таблицы истинности.
4. Какие высказывания называют равносильными?
5. Каким законам подчиняются операции над высказываниями?
