На основании аксиом алгебры логики можно вывести ряд теорем и законов.
Идемпотентные законы 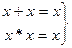 (6)
(6)
Коммутативные законы 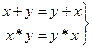 (7)
(7)
Ассоциативные законы  (8)
(8)
Дистрибутивные законы  (9)
(9)
Законы отрицания 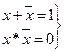 (10)
(10)
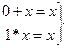 (11)
(11)
 (12)
(12)
Законы двойственности (теоремы де Моргана)
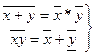 (13)
(13)
Закон двойного отрицания 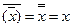 (14)
(14)
Законы поглощения 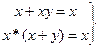 (15)
(15)
Операции склеивания 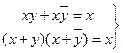 (16)
(16)
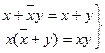 (17)
(17)
Большинство теорем, а также аксиом записаны парами. При внимательном изучении пар можно вывести принцип двойственности– если в тождестве произвести взаимные замены операций дизъюнкции и конъюнкции, а также элементы 0 и 1, если они имеются, то получим тоже тождество. Такое свойство называется принципом двойственности.
f(v,0,l/+,&)=g(v,0,/+,&) где v=(xn-1,...,x0) то справедливо также тождество: f(v,l,0/&,+)=g(v,l,0/&,+)
Все теоремы могут быть доказаны аналитически или методом перебора.
Метод перебора – тождество (13)
Аналитический метод – тождество (17)
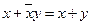
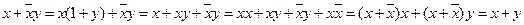
Порядок выполнения операций:
отрицание слагаемой или сомножителя;
конъюнкция сомножителей;
дизъюнкция слагаемых;
общее отрицание дизъюнкции или конъюнкции.