1) Производная суммы функций есть сумма производных.
Пусть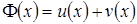 
, тогда
.
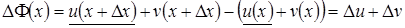Очевидно,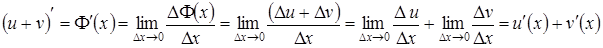 
.
2) 
.
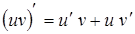3) 
.
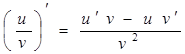Свойства 2) и 3) доказываются аналогично.
4) Если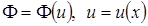 
, то есть функция сложная 
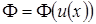, ее производная вычисляется по формуле 
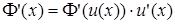. Здесь нижний индекс показывает переменную, по которой происходит дифференцирование.
Докажем это утверждение
.
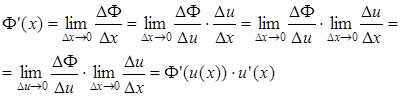В ходе доказательства был осуществлен переход от 
к 
, что является оправданным, поскольку функция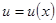 
предполагается дифференцируемой, следовательно, непрерывной.
Производная обратной функции
Дана функция 
и обратная ей функция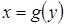 
, т.е. 
. Если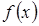 
дифференцируема в точке x и 
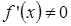,тогда 
дифференцируема в точке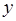 
, при этом 
.
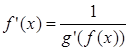Действительно, т.к. 
значит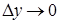 
, о чем говорилось выше, причем оба приращения не равны нулю. Теперь
.
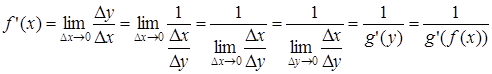