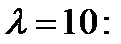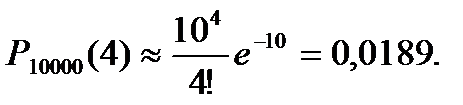Теорема Пуассона. При неограниченном увеличении числа n независимых испытаний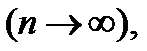 
в каждом из которых может наступить некоторое событие 
с одной и той же вероятностью 
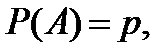стремящейся к нулю 
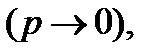при этом 
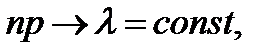вероятность того, что событие 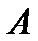наступит m, приближенно равна:
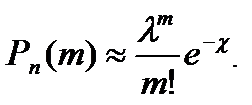(3.22)
Формулу (3.22) называют формулой Пуассона. Эта приближенная формула дает незначительные погрешности, если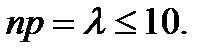 
Значения функции Пуассона 
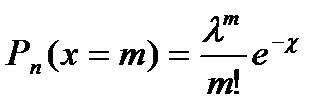находят в таблице, приведенной в приложении 3, на пересечении соответствующих значени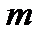й 
и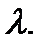 
Пример 3.40. Известно, что на 10000 выпущенных деталей приходится 10 бракованных. Какова вероятность того, что четыре случайно выбранные детали окажутся бракованными?
По условию задачи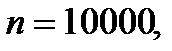 
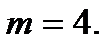Вероятность случайного выбора бракованной детали 
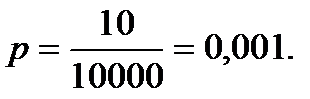Так как значение 
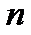велико, а 
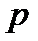− мало и 
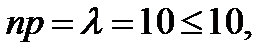воспользуемся (3.22) и найдем значение функции Пуассона из таблицы (приложение 3) для значени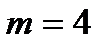й 
и 
