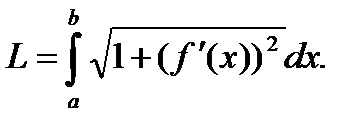1. Формула Ньютона–Лейбница:
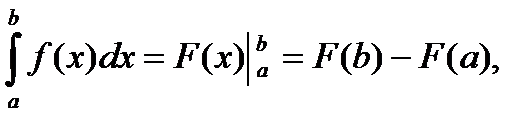
где F′(x) = f(x).
2. Замена переменной:

где x = 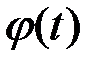 – функция, непрерывная вместе с
– функция, непрерывная вместе с 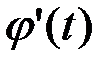 на отрезке
на отрезке 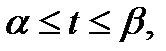
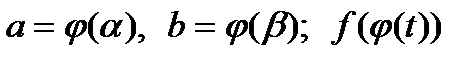 – функция, непрерывная на отрезке
– функция, непрерывная на отрезке 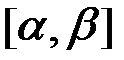 .
.
3. Интегрирование по частям: 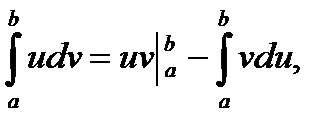
где u = u(x), v = v(x) – дифференцируемые на [a, b] функции.
4. Если f(x) – нечетная функция, то 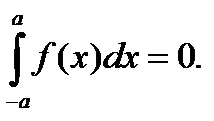
5. Если f(x) – четная функция, то 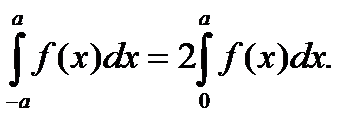
Примеры.
1) 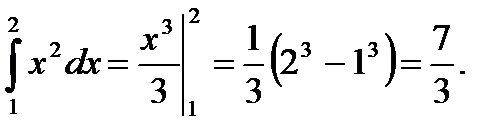
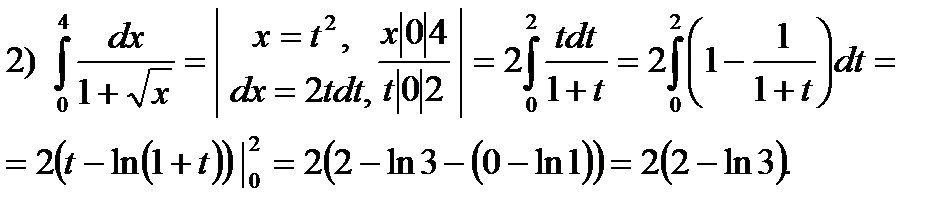

2.58. Вычислить интегралы:
1) 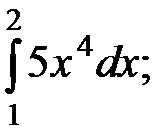 2)
2) 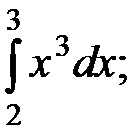 3)
3) 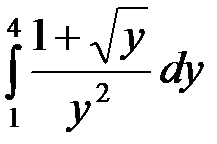 ; 4)
; 4) 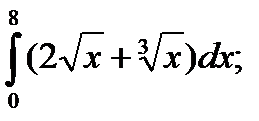
5) 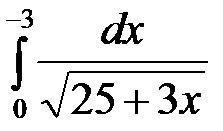 ; 6)
; 6)  7)
7) 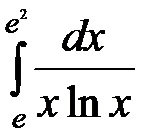 ; 8)
; 8) 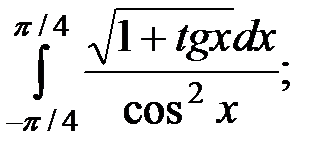
9)  10)
10) 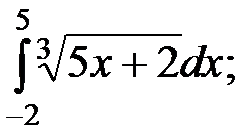 11)
11) 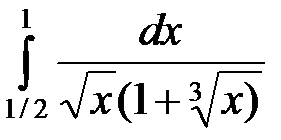 ; 12)
; 12) 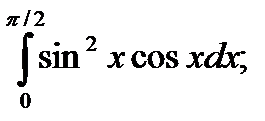
13) 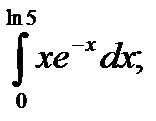 14)
14) 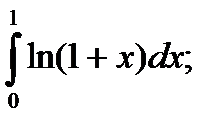 15)
15) 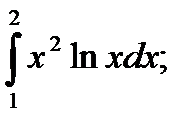 16)
16) 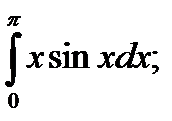
17) 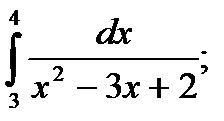 18)
18) 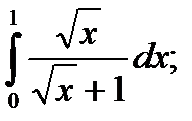 19)
19) 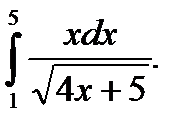
Геометрические приложения определенного интеграла
Пример 2.6.
Найти площадь фигуры, ограниченной линиями у = х2, х = у2.
Решение.
Графики функций пересекаются в точках (0; 0), (1; 1) (рис. 2.3).
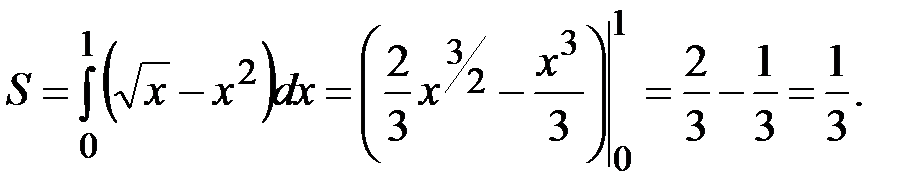
Рис. 2.3. Площадь фигуры
2.59. Найти площадь фигуры, ограниченной графиками функций:
1) 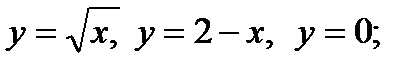 2)
2) 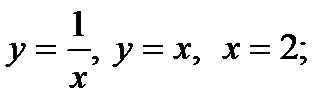
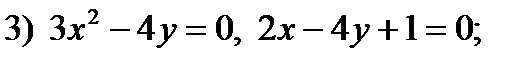
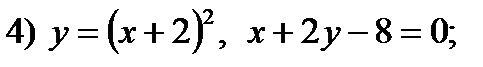
5)  ; 6)
; 6) 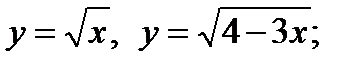
7) 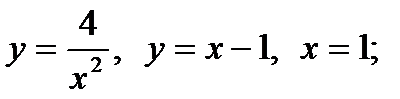 8)
8) 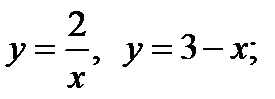
9) 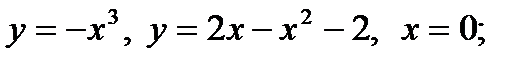 10)
10) 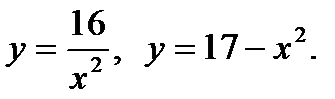
2.60. Найти объем тела, образованного вращением вокруг осей Ох и Оу плоской фигуры, ограниченной линиями:
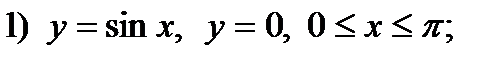 2)
2) 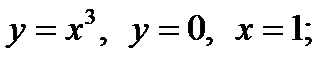
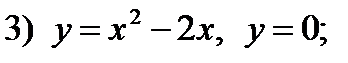 4)
4) 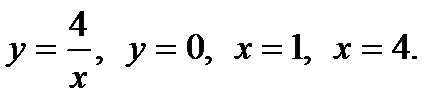
Указание. Объем тела, образованного вращением плоской фигуры вокруг осей координат Ох и Оу, соответственно равен:

2.61. Найти длину дуги кривой:
1) 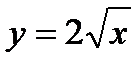 от х = 0 до х = 1; 2)
от х = 0 до х = 1; 2) 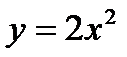 от х = 0 до х = 1;
от х = 0 до х = 1;
3) 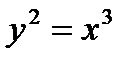 от точки О(0; 0) до точки А(4; 8).
от точки О(0; 0) до точки А(4; 8).
Указание. Длина дуги кривой 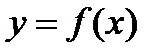 при
при 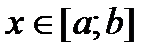 равна
равна