Определение. Матрица А–1 называется обратной к матрице А, если А٠А–1 = А–1٠А = Е.
Теорема. Для любой невырожденной квадратной матрицы существует единственная обратная матрица.
Обратная матрица находится по формуле:
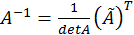 , где Т – транспонирование матрицы, а
, где Т – транспонирование матрицы, а  – присоединенная матица, состоящая из алгебраических дополнений. Аij – это определитель матрицы меньшего порядка, получаемый из матрицы А вычеркиванием i-строки и j-го столбца, взятый со знаком
– присоединенная матица, состоящая из алгебраических дополнений. Аij – это определитель матрицы меньшего порядка, получаемый из матрицы А вычеркиванием i-строки и j-го столбца, взятый со знаком 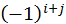 .
.
Для матриц размера  обратная матрица может быть найдена по формуле:
обратная матрица может быть найдена по формуле:

1.6. Найти обратные матрицы для следующих матриц (табл. 1.4)
Таблица 1.4
| №
|
|
|
|
|
|
| Матрица
| 1 2
3 4
| 3 4
5 7
| –3 2 4
2 1 0
1 0 1
| 2 5 7
6 3 4
5 –2 –2
| 1 2 3
0 1 2
0 0 1
|
1.7. При каких значениях 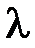 матрица А не имеет обратной:
матрица А не имеет обратной:
1) 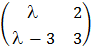 ; 2)
; 2) 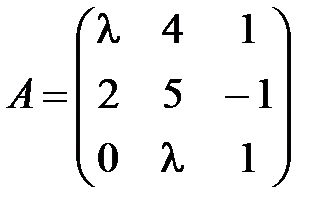 ;
;  3)
3) 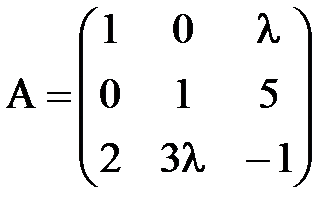 .
.
Пример 1.5. Решение матричного уравнения.
Пусть дано матричное уравнение 
Нужно найти матрицу Х.
Обозначим А = 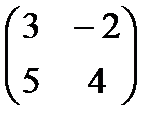 , а В =
, а В =  , тогда имеем уравнение Х ٠ А = В. Умножим обе части справа на А–1:
, тогда имеем уравнение Х ٠ А = В. Умножим обе части справа на А–1:
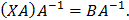 Применяя ассоциативность умножения матриц,
Применяя ассоциативность умножения матриц,
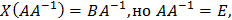
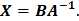
При решении матричных уравнений важно следить за тем, с какой стороны нужно умножать, в силу неперестановочности умножения матриц.
Найдем матрицу А–1, предварительно вычислим определитель:
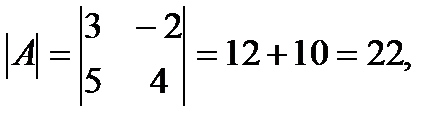
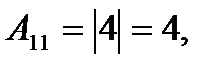
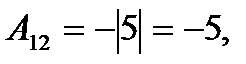

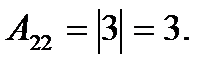
Найдем А 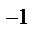 =
= 
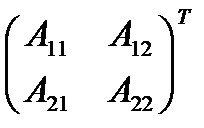 =
= 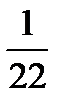
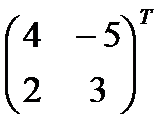 =
= 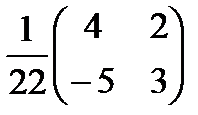 .
.
Итак, 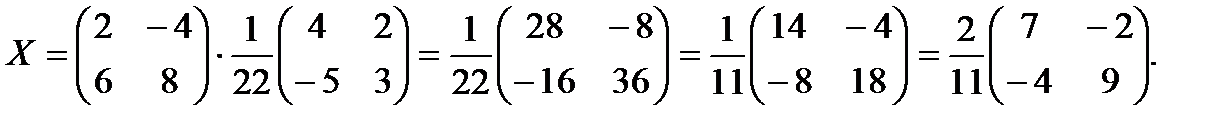
Проверка:  – верно.
– верно.
1.8. Решить матричное уравнение:
1) 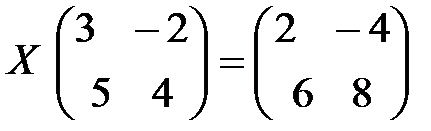 ; 2)
; 2) 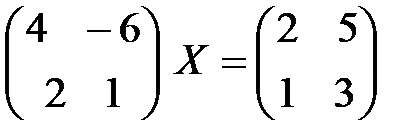 ;
;
3) 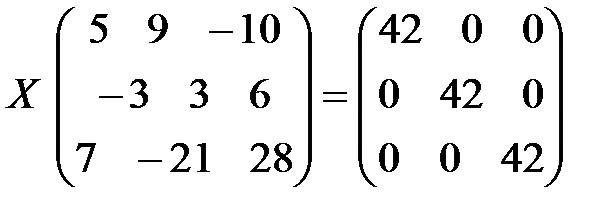 ; 4)
; 4) 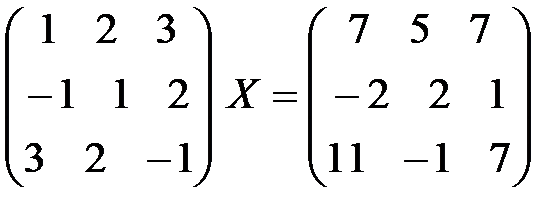 ;
;
5) 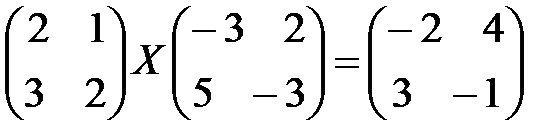 ; 6)
; 6)  .
.