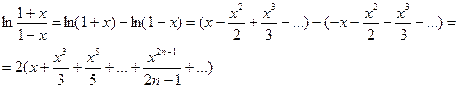Для разложения функции в ряд Маклорена нужно:
1) найти производные 
;
2) вычислить значения производных в точке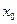 
=0;
3) написать ряд Маклорена для заданной функции и найти его интервал сходимости
4) если в интервале сходимости 
, сумма ряда и функция совпадают в этом интервале.
Таблица разложения некоторых элементарных функций в ряд Маклорена
1) 
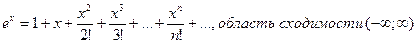
2) 
3) 
4) 
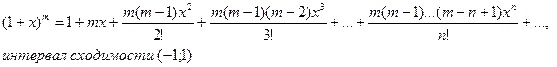
Этот ряд называется биноминальным. На концах интервала при 
cходимость ряда зависит от конкретных значений m:
Если m – целое положительное число, то биноминальный ряд представляет собой формулу бинома Ньютона, так как при n=m+1, n-й член ряда и все последующие члены равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма.
5) 
6) 
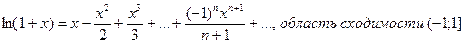
7) 
8) 
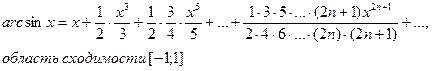
Пример .Разложить в ряд функции а)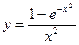 
; б) 
Решение: а) Используем ряд 
, заменяя 
: 
;
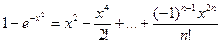
и, наконец,
Область сходимости ряда (-∞; ∞).
б) В разложении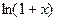 
заменим х на (-х):
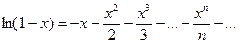
Теперь:
