Совокупность всех первообразных функции f(x) на интервале (a; b) называется неопределенным интегралом от функции f(x) на этом интервале и обозначается формулой:
(1.1)
В формуле (1.1) знак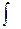 
называется знаком интеграла, выражение f(x)dx -подынтегральным выражением, сама функция f(x) – подынтегральной функцией, переменная х – переменной интегрирования.
Подчеркнем, что если первообразная функции f(x) на интервале (a;b) (а стало быть, и неопределенный интеграл от этой функции) существует, то в формуле (1.1) подынтегральное выражение f(x)dx равно дифференциалу dF(x) любой из первообразных F(x) функции f(x).
На вопрос о существовании у функции f(x) первообразной и неопределенного интеграла отвечает следующая теорема.
Теорема 2 (Теорема Коши). У любой непрерывной на интервале (a; b) функции f(x) существует на этом интервале первообразная и неопределенный интеграл.
Операция нахождения неопределенного интеграла от функции f(x) называется интегрированием этой функции.
Геометрически неопределенный интеграл представляет собой семейство “параллельных” кривых y=F(x)+C. Каждому значению С соответствует определенная кривая семейства. График каждой первообразной называется интегральной кривой.
