Рассмотрим случай, когда частные функции в целевой функции являются гиперболическими функциямис разными степенями, а частные функции в функции-ограничении являются логарифмическими Пусть 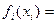
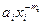 ,
, 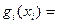
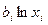 ,
,  ,
, 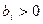 ,
, 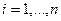 . Решение ищем в области
. Решение ищем в области 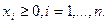 Тогда в соответствии с замечанием 2.1 п. 2 имеем
Тогда в соответствии с замечанием 2.1 п. 2 имеем
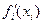 +
+ 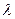
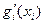 =0,
=0, 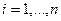 , (1)
, (1)
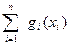 =
= 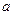 ,
,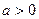 . (2)
. (2)
Подставляя в (1) конкретный вид частных функций в целевой функции и ограничении, получаем
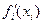 /
/ 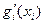 = -
= - 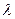


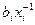 =
= 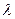 .
.
Отсюда 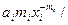
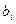 =
= 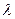

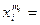
 (
( 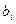
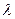 ) или
) или
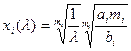 . (3)
. (3)
Подставляя (2) в (2) п. 2, получаем
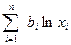 =
= 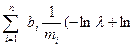

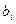 ) =
) = 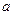 . (4)
. (4)
Отсюда 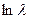 = (
= (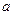 +
+ 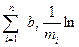

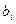 )(
)( 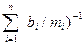 или
или
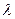 =
= 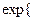 (-
(-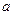 +
+ 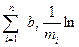

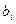 )(
)( 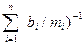
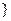 . (5)
. (5)
Подставляя (5) в (3), получаем оптимальные значения 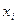
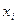
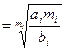
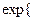
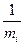 (
(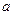 -
- 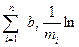

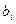 )(
)( 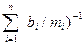
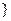 . (6)
. (6)
Тем самым решение оптимальной задачи найдено.
Рассмотрим двойственную задачу. Пусть 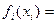
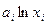 ,
, 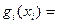
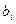
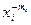 ,
,  ,
, 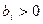 ,
, 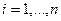 . Решение ищем в области
. Решение ищем в области 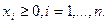 Тогда
Тогда
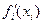 /
/ 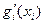 = -
= - 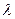

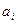
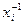 /
/ 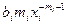 =
= 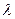 . (7)
. (7)
Из (7) имеем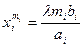 . Отсюда
. Отсюда
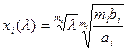 . (8)
. (8)
Подставляя (8) в (2) п. 2, получаем
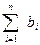
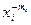 =
= 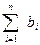 (
( 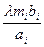
 =
= 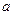 .
.
Отсюда 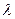 равно
равно
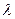 =
= 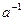 (
( 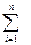
 )
)  . (9)
. (9)
Тогда оптимальные значения 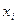 равны
равны
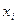 =
=  )(
)( 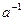 (
( 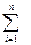
 )
)  )
) 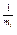 . (10)
. (10)
Тем самым решение оптимальной двойственной задачи найдено.