Рассмотрим теперь случай, когда частные функции в целевой функции и в функции-ограничении являются экспоненциальными функциями. Пусть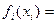 
, 
, 
, 
, 
, 
, 
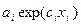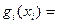
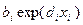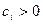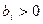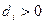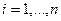. Решение ищем в области 
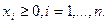Тогда
/ 
= 
/ 
= 
/ 
= 
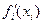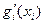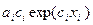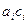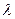. (1)
Отсюда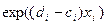 
= / 
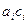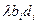или
/ 
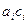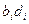) . (2)
Подставляя (2) в (2) п. 2, получаем
/ )) = ( / ) 
= 
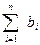
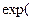
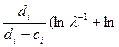
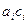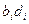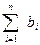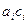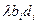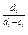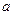. (3)
Пусть 
не зависит от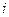 
и = 
. Тогда из (3) получаем
( / ) 
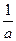
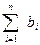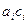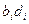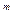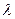
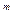= или
=( ( / ) ) 
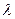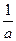
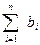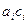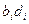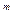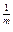. (4)
Подставляя (4) в (2), получаем оптимальные значения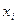 
= 
/ )(( ( / ) ) ) 
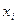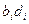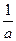
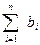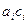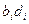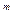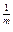. (5)
Тем самым решение оптимальной задачи найдено.
Рассмотрим двойственную задачу. Легко видеть, что она сводится к предыдущей задаче путем замены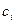 
на 
и наоборот.
