Рассмотрим в качестве частных функций целевой функции логарифмические функции от линейных функций, а в качестве частных функций функции – ограничения – линейные функции. Имеем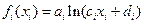 
, здесь предполагается, что 
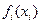является неотрицательной функцией при 
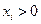, отсюда следует, что должно выполняться неравенство 
, 
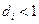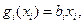
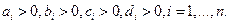Тогда получаем для нахождения оптимальных 
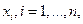и неопределенного множителя Лагранжа 
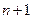уравнение
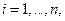(1)
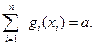(2)
Подставляя в (1) конкретные выражения для 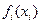и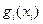 
, находим
,
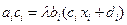откуда
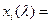
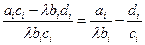. (3)
Подставляя (3) в (2), имеем
откуда
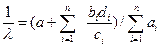. (4)
Подставляя (4) в (3), получаем оптимальные значения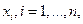
, 
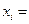
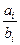
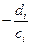(5)
Если все 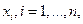полученные по формуле (5) больше нуля, то решение оптимальной задачи найдено, если хотя бы одна переменная из 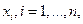не удовлетворяет этому условию, значит при данных исходных данных решения оптимальной задачи в области 
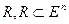, не существует.
Рассмотрим двойственную задачу.
