Имеется дифференцируемая функция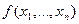 
. Надо найти ее минимум при ограничении 
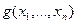= 0. В соответствии с методом неопределенных множителей Лагранжа задача сводится в этом случае к введению переменной 
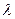и решению следующей оптимальной задачи безусловной оптимизации: найти 
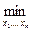
, где = - .
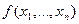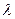
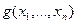В соответствии с теоремой 2 в качестве области 
можно взять область, описываемую следующими неравенствами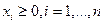 
, и функция 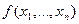должна быть выпукла в области 
. Из теоремы 2 следует требование выпуклости функции 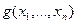только в окрестности точки экстремума 
. В соответствии с этой теоремой надо найти критическую (стационарную) точку и проверить выпуклость функции 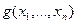в окрестности этой точки.
Тогда по теореме 2 решение этой оптимальной задачи сводится к решению следующей системы в общем виде нелинейных уравнений
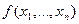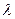
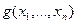= - = 0, 
, 
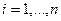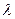
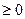, (1)
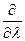
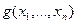= = 0. (2)
Нашей целью является найти те классы функци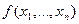й и 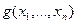, для которых возможно получение аналитических решений, чтобы дать в руки читателей аппарат получения аналитических решений оптимальных задач.
Для удовлетворения условия 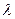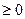величина 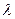должна иметь знак, равный
- 
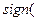
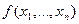
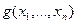). (3)
