Рассмотрим следующий частный случай полинома произвольной степени от двух переменных
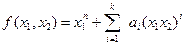. (1)
1. Пусть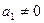 
. Приравнивая частные производные первого порядка от 
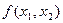нулю, получаем следующую систему уравнений
= 
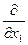
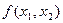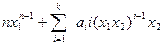= 0, (2)
= 
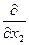
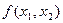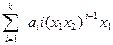= 0. (3)
Единственным решением системы уравнений (2-3) является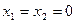 
.
Действительно, легко проверить, что 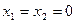является решением системы уравнений (2-3). Рассмотрим, есть ли другие решения. Если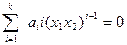 
при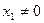 
, то при этом условии (2) не равно нулю, т.е. это решение не проходит. Матрица Гессе имеет следующий вид
.
Её определитель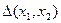 
в этом случае равен
= ( 
)( 
) –
( 
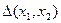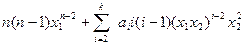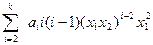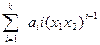
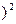. (4)
Его главный минор порядка 1 равен ( ).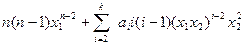
В точке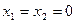 
= - 
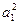, а его главный минор порядка 1 равен 0. Это противоречит п. 2.2. Следовательно, в этом случае решения оптимальной задачи нет.
2. Пусть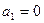 
. Система уравнений (2-3) остается справедливой и в этом случае с учетом приведенного условия. Тогда 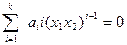при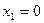 
и система (2-3) справедлива при произвольном 
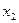. Определитель матрицы Гессе и его главный минор порядка 1 в этом случае равны 0. Это противоречит п. 2.2. Следовательно, и в этом случае решения оптимальной задачи нет.
Методы условной оптимизации
