Алгоритм вычисления нормирующего множителя

Вычисление стационарных вероятностей по формулам (8.12) со­пряжено с трудностью вычисления нормирующего множителя G(K,N). Число операций, требуемых для его определения непосредственно по формуле (2.13) имеет порядок C_N+K-1^N-1. Приведём итеративный алгоритм Бузена, использование которого позволяет значительно сократить объём вычислений. Остановимся сначала на случае, когда m_i=1, i=1, 2, ..., N (СеМО состоит из одноканальных CМО). В этом случае G(K,N) определяется по формуле (8.15).

Введём для любых целых m и n функцию g(m,n) соотношением

g(m,n) = 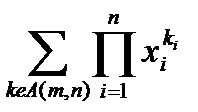, m=0,1, . . . ,K, (8.18)

где A(m,n) = { k= {k₁, k₂,..., k_n}: k_i³0, k_i=m}

Заметим, что A=A(K,N), причём g(K,N)=G(K,N).

Для функции g(m,n) имеем

g(m,n) = + =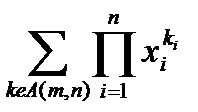

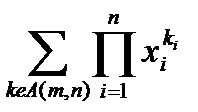k_n=0 k_n³1

= g(m,n-1) + x_ng(m-1,n) . (8.19)

Очевидно, что

g(m,1) = x₁^m , при m = 0, 1, . . . , K (8.20)

g(0,n) = 1 , при n = 0, 1, . . . , N

Если равенствами (8.20)-(8.21) воспользоваться как начальными условиями, то рекуррентная формула (8.19) дает простой алгоритм вычисления функции g(m,n) при любых m и n. Для реализации этого алгоритма при заданных требуется порядка NK операций умножения и NK - сложения.

Теперь рассмотрим общий случай. Положим

g(m,n) = 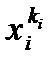/ b_i(k_i). (8.22)

Имеем

g(m,n) = [ 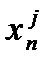/b_n(j) ] g(m-j,n-i). (8.23)

Рекуррентное соотношение (8.23) с очевидными начальными условиями

g(m,1) = 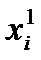/ b₁(m) , m=0,1, …, K;

g(0,n) = 1 , n = 0,1, . . . , N

обеспечивает алгоритм вычисления нормирующего множителя G(K,N) в общем случае.