Пример нахождения наиболее поздних сроков
Пример нахождения наиболее поздних сроков
| s дуг
|
|
|
|
|
|
|
|
|
|
|
|
| 
| 1,2
| 1,6
| 1,7
| 2,3
| 2,7
| 6,7
| 7,3
| 7,5
| 5,3
| 3,4
| 5,4
| 6,5
| 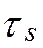
|
|
|
|
|
|
|
|
|
|
|
|
| | i=1,…,7
|
|
|
|
|
|
|
| 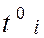
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
| Положим 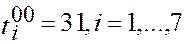
 При первом просмотре очередной дуги s=1,…,12 определяем новые значения по формуле При первом просмотре очередной дуги s=1,…,12 определяем новые значения по формуле 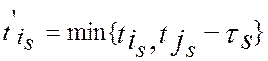 : :
| 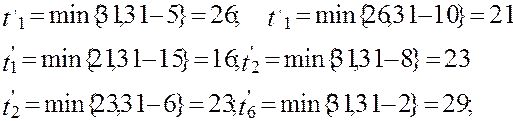
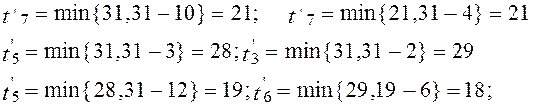
| | | | | | | | | | | | | | | | | s дуг
|
|
|
|
|
|
|
|
|
|
|
|
| 
| 1,2
| 1,6
| 1,7
| 2,3
| 2,7
| 6,7
| 7,3
| 7,5
| 5,3
| 3,4
| 5,4
| 6,5
| 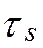
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При втором просмотре дуг получим:
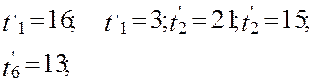
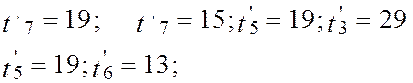 При 3-м просмотре имеем:
При 3-м просмотре имеем: 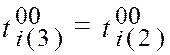 Занесем вычисленные значения в табл.2
Занесем вычисленные значения в табл.2
| | | | | | | | | | | | | | | | Таблица 2
Так как резервы времени 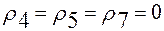 , то события 4, 5, 7 являются критическими. , то события 4, 5, 7 являются критическими.
 Напряженные работы s={3,8,11}: Напряженные работы s={3,8,11}: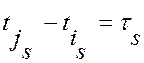 s=3→(1,7): s=3→(1,7): 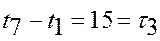 ; s=8→(7,5): ; s=8→(7,5): 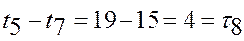 ; s=11→(5,4): ; s=11→(5,4): 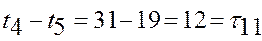 ; ;
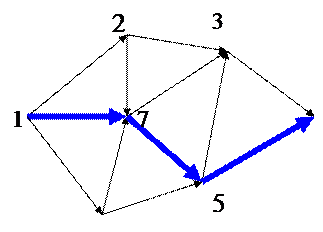
На орграфе соответствующие дуги выделены синим цветом. Путь, содержащий эти дуги – критический. Длина критического пути равна 31.
|