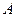Пусть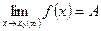 
и 
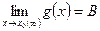. Тогда
1. Функция не может иметь более одного предела.
Предположим, что функция 
при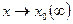 
имеет два предела 
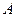и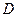 
. Тогда функцию 
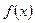можно представить в виде:
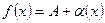
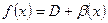, где 
и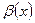 
- бесконечно малые величины.
Найдём разность.
.
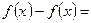
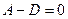
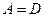2. Предел алгебраической суммы конечного числа функции равен сумме пределов этих функций, т.е.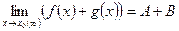 
/
3. Предел произведения конечного числа функции равен произведению пределов этих функций, т.е.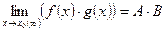 
.
4. Предел частного двух функций равен частному пределов этих функций при условии, что предел знаменателя не равен нулю, т.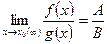е. 
, где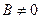 
.
5. Если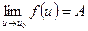 
и
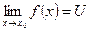, то
.
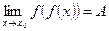6. Если в некоторой окрестности точки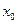 
при достаточно больших 
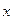имеет место неравенство 
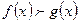, то предел 
.
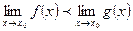Замечание. В теоремах о пределах предполагается существование пределов функци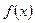и и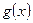 
из чего делается заключение о существование пределов функции их суммы произведения или частного. Однако существование предела суммы произведения или частного конечного числа функции ещё не означает существование пределов самих этих функций.
Пример:
.
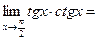
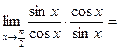
При этом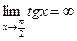 
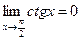
7. 
Если в некоторой окрестности точки 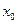функция 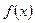заключена между двумя функциям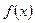и и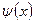 
, т.е. 
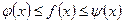, то функция 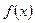имеет тот же предел .
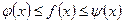