|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Переходный процесс электропривода с двигателем независимого возбуждения при изменении магнитного потокаДата добавления: 2013-12-23; просмотров: 925; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

 возникает когда требуется получить скорость, превышающую основную (согласно требованиям технологического процесса ). Если бы поток изменялся мгновенно, то в начальный момент времени имел бы место бросок тока и момента, как показано на рисунках w=f(Ia) и w=f(M) пунктиром . В действительности Ф изменяется во времени. Поэтому ток якоря и момент двигателя будут изменяться по т.н. динамическим характеристикам (кривая1). Для расчета переходного процесса пренебрегаем индуктивностью якоря LЯ т.к. она мала по сравнению с индуктивностью LВ обмотки возбуждения. Бросок тока и момента будет тем больше, чем быстрее темп изменения Ф. Для получения расчетного выражения воспользуемся уравнением равновесия ЭДС в якорной цепи и уравнением момента.
возникает когда требуется получить скорость, превышающую основную (согласно требованиям технологического процесса ). Если бы поток изменялся мгновенно, то в начальный момент времени имел бы место бросок тока и момента, как показано на рисунках w=f(Ia) и w=f(M) пунктиром . В действительности Ф изменяется во времени. Поэтому ток якоря и момент двигателя будут изменяться по т.н. динамическим характеристикам (кривая1). Для расчета переходного процесса пренебрегаем индуктивностью якоря LЯ т.к. она мала по сравнению с индуктивностью LВ обмотки возбуждения. Бросок тока и момента будет тем больше, чем быстрее темп изменения Ф. Для получения расчетного выражения воспользуемся уравнением равновесия ЭДС в якорной цепи и уравнением момента.

 ;
; 
 ; 2)
; 2) 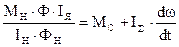
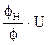 , получим
, получим или в относительных единицах
или в относительных единицах , где
, где  ;
; 
 пределах изменения Ф можно считать, что Ф изменяется по линейному закону, как показано на графике кривой намагничивания. Линейное изменение потока имеет место в случае, если
пределах изменения Ф можно считать, что Ф изменяется по линейному закону, как показано на графике кривой намагничивания. Линейное изменение потока имеет место в случае, если  , т.е. когда цепь машины не насыщена (здесь допускается некоторая погрешность). Закон изменения тока возбуждения при ненасыщенной магнитной цепи можно найти из уравнения равновесия ЭДС для цепи возбуждения
, т.е. когда цепь машины не насыщена (здесь допускается некоторая погрешность). Закон изменения тока возбуждения при ненасыщенной магнитной цепи можно найти из уравнения равновесия ЭДС для цепи возбуждения 
 , где
, где 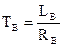
 . Это экспонента.
. Это экспонента. каждом участке длительностью Dt поток j считается постоянным, равным среднему значению
каждом участке длительностью Dt поток j считается постоянным, равным среднему значению  . Аналогично скорость двигателя в течении Dt считаем постоянной и равной среднему значению
. Аналогично скорость двигателя в течении Dt считаем постоянной и равной среднему значению 
 и
и  в уравнение 3 , решаем его относительно
в уравнение 3 , решаем его относительно 


 Расчет кривой скорости ведется с первого участка длительностью Dt, для которого известна
Расчет кривой скорости ведется с первого участка длительностью Dt, для которого известна  и среднее значение потока
и среднее значение потока  . Приращение скорости на первом участке
. Приращение скорости на первом участке 
 . Аналогично определяется приращение скорости на втором участке и т.д. По рассчитанным приращениям строится кривая n=f(t), которая изображена на графике.
. Аналогично определяется приращение скорости на втором участке и т.д. По рассчитанным приращениям строится кривая n=f(t), которая изображена на графике. отсюда
отсюда



