Пусть 
- плоское векторное поле.
Найдем поток векторного поля 
через кривую 
.
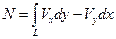
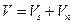
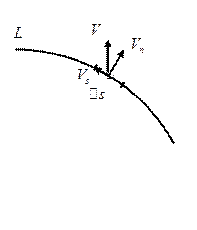
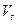- касательная составляющая вектора,
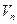- нормальная составляющая вектора.
Элементарный поток проходит через площадку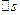 
за единицу времени.
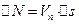
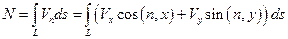
Касательный вектор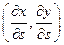 
Нормальный вектор 
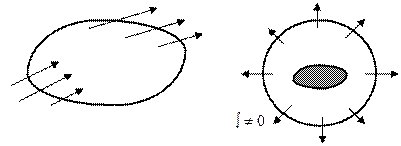
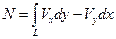
Если кривая - замкнутая
Если поток через любую замкнутую кривую равен нулю, то векторное поле без источников.
Из мат. анализа известно, что если
, то поле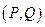 
- потенциальное,
, 
: 
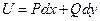
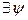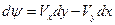
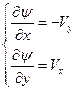
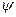- функция тока.
- циркуляция векторного поля (работа) по .
Если - замкнутая кривая, то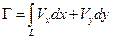 
- настоящая циркуляция.
Если по любой замкнутой кривой циркуляция равна нулю, то говорят, что поле без завихрений и кроме того поле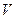 
- потенциальное.
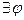- потенциал векторного поля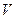
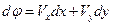
Для 
имеем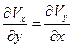 
Для 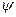имеем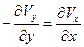 
Уравнение 
- аналитична
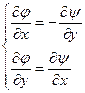
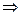
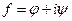- аналитична
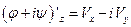- аналитическая
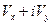- не аналитическая
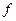- комплексный потенциал
- потенциал для 
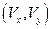
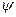- потенциал для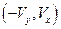 
Функция тока существует всегда, а потенциал (а значит и комплексный потенциал 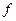) не всегда.
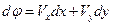существует, если - полный дифференциал, т.е.
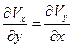
Если 
, то потенциала не существует.
Величина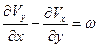 
носит название завихренности.
Вихрь векторного поля
Поле плоское, тогда 
имеет одну ненулевую компоненту
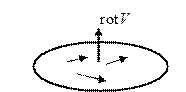Тем не менее, в случае 
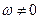можно построить функцию тока .
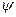1) 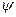- потенциал, т.е.
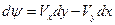, который существует ввиду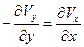
2) Рассмотрим 
Функция 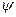удовлетворяет уравнению Пуассона 
.
