Метод последовательного улучшения допустимого вектора (МПУ)

V. Подготовка информации к следующему шагу.

Метод последовательного улучшения допустимого вектора (МПУ)

Метод последовательного улучшения допустимого вектора (МПУ)

IV. Определение 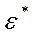(продолжение).

(б) Среди коэффициентов g_k разложения 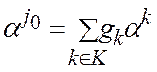имеются положительные. Тогда на основании следствие 2 векторы 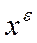являются допустимыми в задаче А лишь при 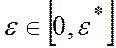, где 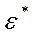вычисляется по формуле:

.

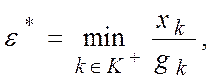
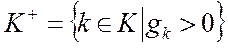При этом фиксируем элемент k*K*, на котором достигается равенство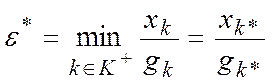, затем переходим к последней процедуре.

В ка­честве нового допустимого базисного множества принимаем

K' = (K\(k*})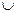{j₀}.

Из базиса удаляется вектор 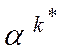, а вводится в базис вектор .

Вычисляем компоненты соответствующего вектора

х(К') = ()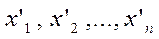

по формулам

, k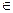K' \{j₀}, .

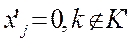При этом

.

Замечание. В процедуре II, вообще говоря, нет не­обходимости вычислять 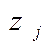для всех 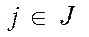. Естественно, для каждой вычисленной величины 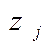сразу же проверить вы­полнение неравенства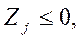 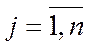. Если это неравенство нару­шается, то имеет место случай б), т.е. К не является двойственно допустимым и вектор не допустимый в задаче А*, вкачестве можно принять соответствующее . Однако ввиду того, что

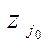должно быть не очень малым. По­этому при решении небольших задач обычно вычис­ляют все величины 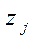и в случае б) индекс 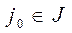выби­рается так, чтобы 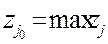. При решении больших задач все 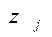уже не вычисляются, но с помощью специальных приемов добиваются того, чтобы для выбранного 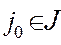в случае б) величина 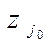мало отличалась от максималь­ного .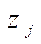