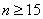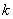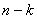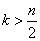I. Коды, исправляющие одиночную ошибку, 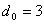 .
.
1. Расчет соотношения между контрольными и информационными символами кода
производится на основании выражений (59) - (69).
Если задано число информационных разрядов 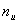
, то число контрольных разрядов 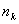
находим из выражения
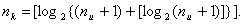
Общее число символов кода
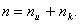
Если задана длина кода 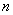 , то число контрольных разрядов
, то число контрольных разрядов
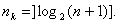
Соотношение числа контрольных и информационных символов для кодов с 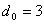
приведены в табл. 3 приложения 9.
2. Выбор образующего многочлена производится по таблицам неприводимых
двоичных многочленов.
Образующий многочлен 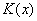
следует выбирать как можно более коротким, но степень его должна быть не меньше
числа контрольных разрядов 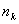
, а число ненулевых членов - не меньше минимального кодового расстояния 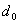
.
3. Выбор параметров единичной транспонированной матрицы происходит из
условия, что число столбцов (строк) матрицы определяется числом информационных
разрядов, т. е. ранг единичной матрицы равен 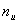
.
4. Определение элементов дополнительной матрицы производится по остаткам
от деления последней строки транспонированной матрицы (единицы с нулями) на
образующий многочлен. Полученные остатки должны удовлетворять следующим
требованиям:
а) число разрядов каждого остатка должно быть равно числу контрольных символов 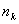
, следовательно, число разрядов дополнительной матрицы должно быть равно степени
образующего многочлена;
б) число остатков должно быть не меньше числа строк единичной транспонированной
матрицы, т. е. должно быть равно числу информационных разрядов 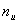
;
в) число единиц каждого остатка, т. е. его вес, должно быть не менее величины 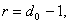
, где 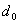 - минимальное
- минимальное
кодовое расстояние, не меньшее числа обнаруживаемых ошибок;
г) количество нулей, приписываемых к единице с нулями при делении ее на
выбранный неприводимый многочлен, должно быть таким, чтобы соблюдались
условия а), б), в).
5. Образующая матрица составляется дописыванием элементов дополнительной
матрицы справа от единичной транспонированной матрицы либо умножением элементов
единичной матрицы на образующий многочлен.
6. Комбинациями искомого кода являются строки образующей матрицы и все
возможные суммы по модулю 2 различных сочетаний строк образующей матрицы.
7. Обнаружение и исправление ошибок производится по остаткам от деления
принятой комбинации 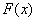
на образующий многочлен 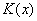
. Если принятая комбинация делится на образующий многочлен без остатка, то код
принят безошибочно. Остаток от деления свидетельствует о наличии ошибки, но
не указывает, какой именно. Для того чтобы найти ошибочный разряд и исправить
его в циклических кодах, осуществляют следующие операции:
а) принятую комбинацию делят на образующий многочлен и
б) подсчитывают количество единиц в остатке (вес остатка).
Если 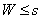 , где s -
, где s -
допустимое число исправляемых данным кодом ошибок, то принятую комбинацию
складывают по модулю 2 с полученным остатком. Сумма даст исправленную
комбинацию. Если 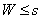
, то
в) производят циклический сдвиг принятой комбинации 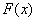
влево на один разряд. Комбинацию, полученную в результате циклического сдвига,
делят на 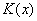 .
.
Если в результате этого повторного деления 
то делимое суммируют с остатком, затем
г) производят циклический сдвиг вправо на один разряд комбинации, полученной в
результате суммирования последнего делимого с последним остатком. Полученная в
результате комбинация уже не содержит ошибок. Если после первого циклического
сдвига и последующего деления остаток получается таким, что его вес 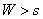
, то
д) повторяют операцию пункта в) до тех пор, пока не будет 
. В этом случае комбинацию, полученную в результате последнего циклического
сдвига, суммируют с остатком от деления этой комбинации на образующий
многочлен, а затем
е) производят циклический сдвиг вправо ровно на столько разрядов, на сколько
была сдвинута суммируемая с последним остатком комбинация относительно принятой
комбинации. В результате получим исправленную комбинацию
[18].
II. Коды, обнаруживающие трехкратные ошибки, 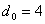 .
.
1. Выбор числа корректирующих разрядов производится из соотношения
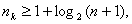
или
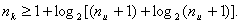
2. Выбор образующего многочлена производят, исходя из
следующих соображений: для обнаружения трехкратной ошибки
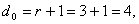
поэтому степень образующего многочлена не может быть меньше четырех; многочлен
третьей степени, имеющий •число ненулевых членов больше или равное трем,
позволяет обнаруживать все двойные ошибки, многочлен первой степени 
обнаруживает любое количество нечетных ошибок, следовательно, многочлен
четвертой степени, получаемый в результате умножения этих многочленов, обладает
их корректирующими свойствами: может обнаруживать две ошибки, а также одну и
три, т. е. все трехкратные ошибки.
3. Построение образующей матрицы производят либо нахождением остатков от
деления единицы с нулями на образующий многочлен, либо умножением строк
единичной матрицы на образующий многочлен.
4. Остальные комбинации корректирующего кода находят суммированием по
модулю 2 всевозможных сочетаний строк образующей матрицы.
5. Обнаружение ошибок производится по остаткам от деления принятой
комбинации 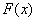 на
на
образующий многочлен 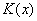
. Если остатка нет, то контрольные разряды отбрасываются и информационная
часть кода используется по назначению. Если в результате деления получается
остаток, то комбинация бракуется. Заметим, что такие коды могут обнаруживать
75% любого количества ошибок, так как кроме двойной ошибки обнаруживаются все
нечетные ошибки, но гарантированное количество ошибок, которое код никогда не
пропустит, равно 3.
Пример: Исходная кодовая комбинация - 0101111000, принятая - 0001011001 (т.
е. произошел тройной сбой). Показать процесс обнаружения ошибки, если
известно, что комбинации кода были образованы при помощи многочлена 101111.
Решение:
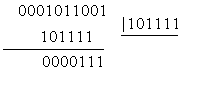
Остаток не нулевой, комбинация бракуется. Указать ошибочные разряды при
трехкратных искажениях такие коды не могут.
III. Циклические коды, исправляющие две и большее количество ошибок, 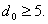
Методика построения циклических кодов с 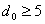
отличается от методики построения циклических кодов с 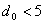
только в выборе образующего многочлена. В литературе эти коды известны как коды
БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем - авторов методики
построения циклических кодов с 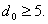
).
Построение образующего многочлена зависит, в основном, от двух параметров: от
длины кодового слова п. и от числа исправляемых ошибок s. Остальные
параметры, участвующие в построении образующего многочлена, в зависимости от
заданных 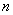 и
и 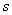
могут быть определены при помощи таблиц и вспомогательных соотношений, о которых
будет сказано ниже.
Для исправления числа ошибок 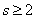
еще не достаточно условия, чтобы между комбинациями кода минимальное кодовое
расстояние  .
.
необходимо также, чтобы длина кода 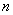
удовлетворяла условию
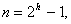 (79)
(79)
при этом п всегда будет нечетным числом. Величина h определяет
выбор числа контрольных символов 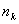
и связана с 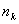 и s
и s
следующим соотношением:
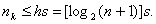 (80)
(80)
С другой стороны, число контрольных символов определяется образующим многочленом
и равно его степени. При больших значениях h длина кода п
становится очень большой, что вызывает вполне определенные трудности при
технической реализации кодирующих и декодирующих устройств. При этом часть
информационных разрядов порой остается неиспользованной. В таких случаях для
определения h удобно пользоваться выражением
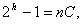 (81)
(81)
где 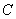 является одним из сомножителей, на которые разлагается число п.
является одним из сомножителей, на которые разлагается число п.
Соотношения между 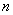 , С и h могут быть сведены в следующую таблицу
, С и h могут быть сведены в следующую таблицу
| № п/п
| h
| 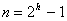
| C
|
|
|
|
|
5; 3
7; 3; 3
17; 5; 3
7; 3; 7
31; 11; 3
89; 23
3; 3; 5; 7; 13
|
Например, при h = 10 длина кодовой комбинации может быть равна и 1023 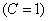
и 341 (С = 3), и 33 (С =31), и 31 (С = 33), понятно, что п не может быть
меньше 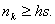 Величина
Величина
С влияет на выбор порядковых номеров минимальных многочленов, так как
индексы первоначально выбранных многочленов умножаются на С.
Построение образующего многочлена 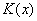
производится при помощи так называемых минимальных многочленов 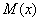
, которые являются простыми неприводимыми многочленами (см. табл. 2,
приложение 9). Образующий многочлен представляет собой произведение нечетных
минимальных многочленов и является их наименьшим общим кратным (НОК).
Максимальный порядок 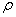
определяет номер последнего из выбираемых табличных минимальных многочленов
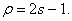 (82)
(82)
Порядок многочлена используется при определении числа сомножителей 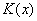
. Например, если s = 6, то 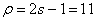
. Так как для построения 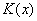
используются только нечетные многочлены, то ими будут: 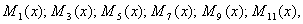
старший из них имеет порядок 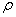
. Как видим, число сомножителей 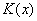
равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных
многочленов, участвующих в построении образующего многочлена,
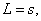 (83)
(83)
а старшая степень
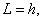 (84)
(84)
(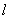 указывает колонку в
указывает колонку в
таблице минимальных многочленов, из которой обычно выбирается многочлен для
построения 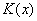 ).
).
Степень образующего многочлена, полученного в результате перемножения
выбранных минимальных многочленов,
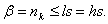 (85)
(85)
В общем виде
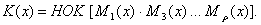 (86)
(86)
Декодирование кодов БЧХ производится по той же методике, что и декодирование
циклических кодов с 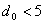
. Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с 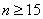
, могут возникнуть весьма сложные варианты, когда для обнаружения и исправления
ошибок необходимо производить большое число циклических сдвигов. В этом случае
для облегчения можно комбинацию, полученную после 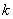
-кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на 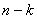
циклических сдвигов. Это целесообразно делать только при 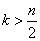
.

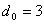 .
.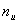
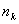
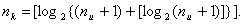
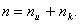
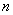 , то число контрольных разрядов
, то число контрольных разрядов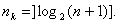
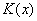
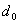
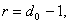
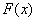
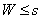 , где s -
, где s -
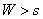
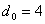 .
.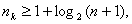
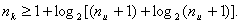
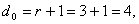

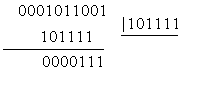
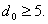
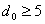
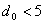
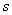
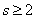
 .
.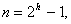 (79)
(79)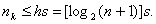 (80)
(80)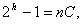 (81)
(81)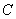 является одним из сомножителей, на которые разлагается число п.
является одним из сомножителей, на которые разлагается число п.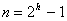
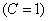
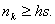 Величина
Величина 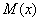
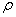
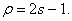 (82)
(82)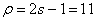
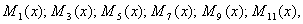
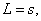 (83)
(83)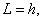 (84)
(84)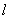 указывает колонку в
указывает колонку в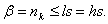 (85)
(85)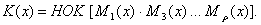 (86)
(86)