Поиск
Простейшие алгоритмы
Лекция 9. Моделирование распределения ресурсов методом динамического программирования.
делении 50 млн. руб. для осуществления инновационных ме-
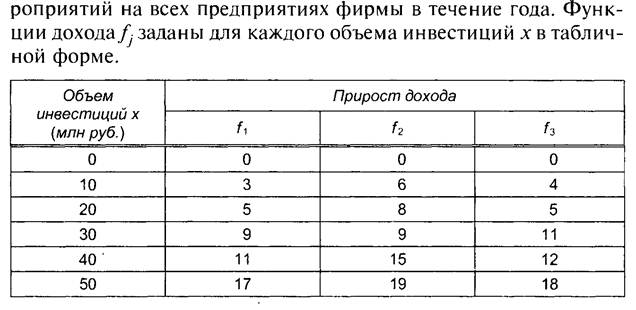
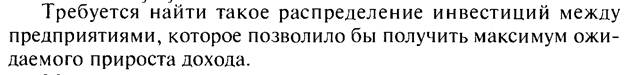
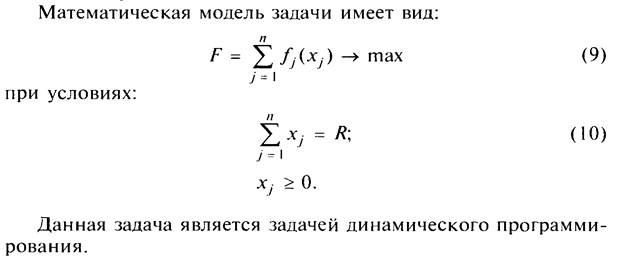
Задача распределения инвестиций может быть представлена в виде графа (сети), вершинами которого являются значения критерия оптимальности (дохода) на соответствующем шаге, а дуги текущие значения дохода каждого предприятия в зависимости от величины вложенных инвестиций. Исходная вершина F0=0, соответствует начальному состоянию, когда инвестиции еще не распределяются. Сечение F1 графа, соответствует распределению инвестиций для одного предприятия, сечение F2 – для двух предприятий, вершина F3 =20 – итоговому значению критерия для трех предприятий.
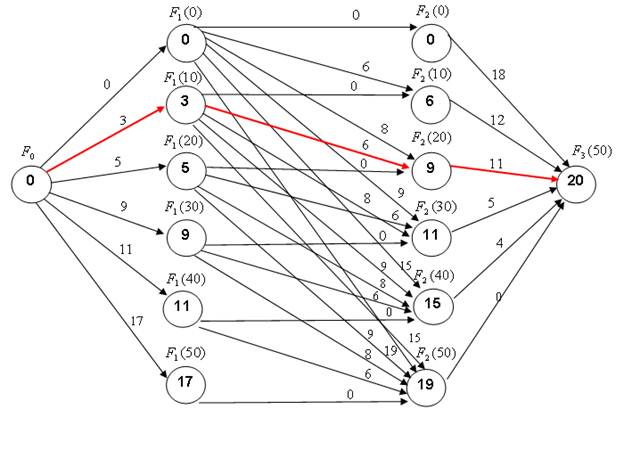
Рис.6.1 Представление задачи распределения инвестиций между предприятиями в виде сети
В массиве A: array[iMin..iMax] of ТИП найти элемент равный B.
Листинг. Алгоритм линейного поиска
i:=iMin;
while (i<iMax) and (A[i]=B) do i:=i+1;
Цикл while завершит свою работу либо при нахождении элемента равного B, либо при переборе всех элементов массива.
На каждом шаге цикла выполняется две проверки. Для упрощения проверок в конец массива A: array[iMin..iMax+1] of ТИП добавляется барьер - элемент равный B.
Листинг. Алгоритм линейного поиска с барьером
i:=iMin; A[iMax+1]:=B;
while A[i]=B do i:=i+1;
Завершение работы цикла гарантировано, т.к. элемент B в массиве всегда есть. Ожидаемое число шагов – N/2.
