Правило (принцип оптимальности по Беллману).
На любом k-ом шаге решение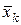 
надо выбрать таким, чтобы было возможно выбрать последующие решения 
, для которых были бы максимальны как 
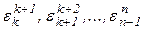, так и 
.
Осуществление принципа Беллмана производится пошагово, «впопятную». Именно, вначале оценивается решение в момент времени tn-1 (последнее решение):
.
В пространстве решений 
перебираем решения 
. Для каждого состояния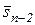 
обозначим:
,
эффективность 
достигается выбором решения 
, которое называется условно оптимальным (при условии, что система находится в состоянии 
);
. Допустим, что состояние соответствует состоянию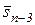 
и решению 
.
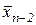Отступая назад на один шаг, находим:
;
значение 
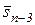зависит только от , так как , 
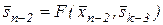по модели управления системой.
Повторяем процедуру вплоть до вовлечения в выбор решения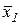 
:
– это и есть уравнение Беллмана, воплощение принципа Беллмана. Таким образом находится набор оптимальных решений 
как функций аргументов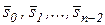 
соответственно, определяемых в обратном порядке (от к 
). Зная значение 
и функцию 
, находится значение вектора решения; по модели управления определяется следующее состояние системы 
, по нему находится значение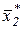 
и так далее.
Уравнение Беллмана можно переписать в виде:
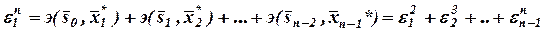, демонстрирующим аддитивные свойства оптимальной эффективности.
