Урок 7 - Графіки в Matlab. Побудова графіків і таблиць в Матлабе

1. Побудова таблиць значень функції однієї змінної в пакеті MatLab

Відображення функції у вигляді таблиці зручно, якщо є порівняно невелике число значень функції. Нехай потрібно вивести в командне вікно таблицю значень функції

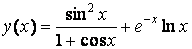
у точках 0.2, 0.3, 0.5, 0.8, 1.3, 1.7, 2.5.
Завдання вирішується в два етапи.
1. Створюється вектор-рядок х, містить координати заданих точок.
2. Обчислюються значення функції y(х)від кожного елемента вектора х і записуються отримані значення в вектор-рядок .
Значення функції необхідно знайти для кожного з елементів вектор-рядки х, тому операції вираз для функції повинні виконуватися поелементно.

» х = [0.2 0.3 0.5 0.8 1.3 1.7 2.5]
х =
0.2000 0.3000 0.5000 0.8000 1.3000 1.7000 2.5000 » y = sin(x).^2./(l+cos(x))+exp(-x).*log(x)
У =
-1.2978-0.8473-0.2980 0.2030 0.8040 1.2258 1.8764

Зверніть увагу, що при спробі використання операцій зведення в ступінь ^, ділення та множення * (які не належать до поелементним) виводиться повідомлення про помилку вже при зведенні sin(x) у квадрат:

» y = sin(х)^2/(1+соз(х))+exp(-x)*log(x)
??? Error using ==> ^
Matrix must be square.

Справа в тому, що в MatLab операції * і ^ застосовуються для перемноження матриць відповідних розмірів і зведення квадратної матриці у ступінь.
Таблиці можна надати більш зручний для читання вигляд, розташувавши значення функції безпосередньо під значеннями аргументу:

» х
х =
0.2000 0.3000 0.5000 0.8000 1.3000 1.7000 2.5000 » у
у =
-1.2978-0.8473-0.2980 0.2030 0.8040 1.2258 1.8764

Часто потрібно вивести значення функції в точках відрізка, віддалених один від одного на рівну відстань (крок). Припустимо, що необхідно вивести таблицю значень функції y(х)наотрезке [1, 2] з кроком 0.2. Можна, звичайно, ввести вектор-рядок значень аргументу х=[1, 1.2, 1.4, 1.6, 1.8, 2.0] з командного рядка і обчислити всі значення функції так, як описано вище. Однак, якщо крок буде не 0.2, а, наприклад 0.01, то чекає велика робота по введенню вектора х.
В MatLab передбачено просте створення векторів, кожен елемент яких відрізняється від попереднього на постійну величину, тобто на крок. Для введення таких векторів служить двокрапка (не плутайте з індексацією за допомогою двокрапки). Наступні два оператора призводять до формування однакових вектор-рядків. Умовно можна записати

» х = [1, 1.2, 1.4, 1.6, 1.8, 2.0]
х =
1.0000 1.2000 1.4000 1.6000 1.8000 2.0000
» х = [1:0.2:2]
х =
1.0000 1.2000 1.4000 1.6000 1.8000 2.0000

Умовно можна записати

х = [початкове значення : крок : кінцеве значення]

Необов'язково піклуватися про те, щоб сума передостаннього значення кроку дорівнювала б кінцевого значення, наприклад, при виконанні наступного оператора присвоювання

» х = [1:0.2:1.9]
х =
1.0000 1.2000 1.4000 1.6000 1.8000

Вектор-рядок заповниться до елемента, не перевершує певний нами кінцеве значення. Крок може бути і негативним:

» х = [1.9:-0.2:1]
х =
1.9000 1.7000 1.5000 1.3000 1.1000

У разі негативного кроки для отримання непустий вектор-рядки початкове значення повинно бути більше кінцевого.
Для заповнення вектор-стовпчика елементами, що починаються з нуля і закінчуються 0.5 з кроком 0.1, слід заповнити вектор-рядок, а потім використовувати операцію транспонування:

» х = [0:0.1:0.5]"
х =
0
0.1000
0.2000
0.3000
0.4000
0.5000

Зверніть увагу, що елементи вектора, заповнюємо за допомогою двокрапки, можуть бути тільки речовими, тому для транспонування можна використовувати апостроф замість точки з апострофом.
Крок, що дорівнює одиниці, допускається не вказувати при автоматичному заповненні:

» х = [1:5]
х =
1 2 3 4 5

Нехай потрібно вивести таблицю значень функції

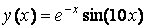
на відрізку [0, 1] з кроком 0.05,
Для виконання цього завдання необхідно виконати наступні дії:
1. Сформувати вектор-рядок х за допомогою двокрапки.
2. Обчислити значення (х)отэлементов х.
3. Записати результат в вектор-рядок y.
4. Вивести хі .

» х = [0:0.05:1];
» = ехр(-х).*sin(10*x);
» х
х =
Columns 1 through 7
Про 0.0500 0.1000 0.1500 0.2000 0.2500 0.3000
Columns 8 through 14
0.3500 0.4000 0.4500 0.5000 0.5500 0.6000 0.6500
Columns 15 through 21
0.7000 0.7500 0.8000 0.8500 0.9000 0.9500 1.0000
» у
У =
Columns 1 through 7
0 0.4560 0.7614 0.8586 0.7445 0.4661 0.1045
Columns 8 through 14
-0.2472-0.5073-0.6233-0.5816-0.4071-0.1533 0.1123
Columns 15 through 21
0.3262 0.4431 0.4445 0.3413 0.1676-0.0291-0.2001

Вектор-рядки x і yскладаються з двадцяти одного елемента, і не поміщається на екрані в один рядок, тому виводяться по частинах. Так як х іy зберігаються в двовимірних масивах розмірністю один на двадцять один, то виводяться по стовпцях, кожен з яких складається з одного елемента. Спочатку виводяться стовпчики з першого по сьомий (columns 1 through 7), потім - з восьмого за чотирнадцятий (columns 8 through 14), і нарешті - з п'ятнадцятого по двадцять перший (columns 15 through 21). Більш наочним і зручним є графічне представлення функції.

2. Побудова графіків функцій однієї змінної

2.1. Графіки функцій в лінійному масштабі

MatLab має добре розвиненими графічними можливостями для візуалізації даних. Розглянемо на початку побудова найпростішого графіка функції однієї змінної на прикладі функції

,

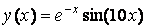певної на відрізку [0, 1]. Висновок функції у вигляді графіка складається з наступних етапів:
1. Завдання вектора значень аргументу х.
2. Обчислення вектора значень функції y(х).
3. Виклик команди plot для побудови графіка.
Команди для завдання вектора х та обчислення функції краще завершувати крапкою з комою для придушення виводу у командне вікно їх значень (після команди plot крапку з комою ставити необов'язково, оскільки вона нічого не виводить в командне вікно).

» х = [0:0.05:1];
» = ехр(-х).*sin(10*x);
» plot(x, y)

Після виконання команд на екрані з'являється вікно Figure No. 1 з графіком функції. Вікно містить меню, панель інструментів та область графіка. Надалі будуть описані команди, спеціально призначені для оформлення графіка. Зараз нас цікавить сам принцип побудови графіків і деякі прості можливості візуалізації функцій.
Для побудови графіка функції в робочому середовищі MatLab повинні бути визначені два вектори однаковою розмірності, наприклад х і . Відповідний масив х містить значення аргументів, а у - значення функції від цих аргументів. Команда plot з'єднує точки з координатами (x(i), y(i)) прямими лініями, автоматично масштабируя осі для оптимального розташування графіку у вікні. При побудові графіків зручно розташувати на екрані основне вікно MatLab і вікно з графіком поруч так, щоб вони не перекривали.
Побудований графік функції має злами. Для більш точного побудови графіка функцію необхідно обчислити y(х) у більшій кількості точок на відрізку [0, 1], тобто поставити менший крок при введенні вектора х:

» х = [0:0.01:1];
» = ехр(-х).*sin(10*x);
» plot(x, y)

У результаті виходить графік функції у вигляді більш плавною кривої.
Порівняння декількох функцій зручно робити, відобразивши їх графіки на одних осях. Наприклад, побудуємо на відрізку [-1, -0.3] графіки функцій
,

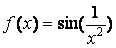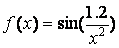
за допомогою наступної послідовності команд:

» х = [-1:0.005:-0.3];
» f = sin(x.^-2);
» g = sin(1.2*x.^-2);
» plot(x, f, x, g)

Функції необов ’ язково повинні бути визначені на одному і тому ж відрізку. У цьому випадку при побудові графіків MatLab вибирає максимальний відрізок, що містить інші. Важливо тільки в кожній парі векторів абсцис і ординат вказати відповідні один одному вектора, наприклад:

» х1 = [-1:0.005:-0.3];
» f = sin(x1.^-2);
» х2 = [-1:0.005:0.3];
» g = sin(1.2*x2.^-2);
» plot(x1, f, x2, g)

Аналогічним чином за допомогою завдання в plot через кому пар аргументів виду: вектор абсцис, вектор ординат, здійснюється побудова графіків довільного числа функцій.

Примітка 1

Використання plot з одним аргументом - вектором - призводить до побудови "графіка вектора", тобто залежності значень елементів вектора від їх номерів. Аргументом plot може бути і матриця, в цьому випадку на одні координатні осі виводяться графіки стовпців.
Іноді потрібно порівняти поведінку двох функцій, значення яких сильно відрізняються один від одного. Графік функції з невеликими значеннями практично зливається з віссю абсцис, і встановити його вигляд не вдається. У цій ситуації допомагає функція plotyy, яка виводить графіки у вікно з двома вертикальними осями, що мають відповідний масштаб.
Порівняйте, наприклад, дві функці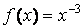ї: і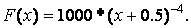

» х = [0.5:0.01:3];
» f = х.^-3;
» F = 1000*(х+0.5).^-4;
» plotyy(x, f, x, F)

При виконанні цього прикладу зверніть увагу, що колір графіка співпадає з кольором відповідної йому осі ординат.
пФункция plot використовує лінійний масштаб по обох координатних осей. Однак MatLab надає користувачеві можливість будувати графіки функцій однієї змінної у логарифмічної або полулогарифмическом масштабі.

2.2. Графіки функцій в логарифмічних масштабах

Для побудови графіків в логарифмічної і полулогарифмическом масштабах служать наступні функції:
- loglog (логарифмічний масштаб по обох осях);
- semilogx (логарифмічний масштаб тільки по осі абсцис);
-semilogy (логарифмічний масштаб тільки по осі ординат).

Аргументи loglog, semilogx і semilogy задаються у вигляді пари векторів значень абсцис і ординат так само, як для функції plot, описаної в попередньому пункті. Побудуємо, наприклад, графіки функцій 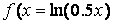і 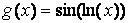на відрізку [0.1, 5] логарифмічної масштабі по осі х:

» х = [0.1:0.01:10];
» f = log(0.5*x);
» g = sin(log(x));
» semilogx(x, f, x ,g)

2.3. Завдання властивостей на графіках функцій

Побудовані графіки функцій повинні бути максимально зручними для сприйняття. Часто потрібно нанести маркери, змінити колір ліній, а при підготовці до монохромного друку - задати тип лінії (суцільна, пунктирна, штрих-пунктирна і т.д.). MatLab надає можливість керувати виглядом графіків, побудованих за допомогою plot, loglog, semilogx і semilogy, для чого служить додатковий аргумент, що пишеться за кожною парою векторів. Цей аргумент полягає в апострофи і складається з трьох символів, які визначають: колір, тип маркера і тип лінії. Використовується одна, дві або три позиції, залежно від необхідних змін. У таблиці наведено можливі значення цього аргументу зі вказівкою результату.

Таблиця

Якщо, наприклад, необхідно побудувати перший графік червоними точковими маркерами без лінії, а другого графік - чорної пунктирною лінією, то слід використовувати команду plot(x, f, "r.", х, g, "k:").

2.4. Оформлення графіків функцій

Зручність використання графіків багато в чому залежить від додаткових елементів оформлення: координатної сітки, підписів до вісі, заголовку та легенди. Сітка наноситься командою grid on, підписи до осях розміщуються за допомогою xlabel, ylabel, заголовок дається командою title. Наявність декількох графіків на одних осях вимагає приміщення легенди командою legend з інформацією про лініях. Всі перераховані команди застосовні до графіків як в лінійному, так і в логарифмічної і полулогарифмическом масштабах. Наступні команди виводять графіки зміни добової температури, які забезпечені всією необхідною інформацією.

» time= [0 4 7 9 10 11 12 13 13.5 14 14.5 15 16 17 18 20 22];
» temp1 = [14 14 15 16 17 18 20 22 24 28 25 20 16 13 13 14 13];
» temp2= [12 13 13 14 16 18 20 20 23 25 25 20 16 12 12 11 10];
» plot(time, temp1, "ro-", time, temp2, "go-")
» grid on
» title"(Добові температури")
» xlabel("Час (год.)")
» ylabel("Температура (С)")
» legend("10 травня, 11 травня")

При додаванні легенди слід врахувати, що порядок і кількість аргументів команди legend повинні відповідати лініях на графіку. Останнім додатковим аргументом може бути положення легенди, графічному вікні:

* -1 - поза графіком у правому верхньому куті графічного вікна;
* 0 - вибирається краще становище в межах графіка так, щоб якомога менше перекривати самі графіки;
* 1 - у верхньому правому куті графіка (це положення використовується за замовчуванням);
* 2 - у верхньому лівому куті графіка;
* 3 - в нижньому лівому куті графіка;
* 4 - в нижньому правому куті графіка.

У заголовку графіка, легенди і підписах осей допускається додавання формул і зміна стилю шрифту при допомоги формату Тих.
MatLab виводить графіки різним кольором. Монохромний принтер надрукує графіки різними відтінками сірого кольору, що не завжди зручно. Команда plot дозволяє легко встановити стиль і колір ліній, наприклад

» plot(x,f,"k",-x,g,"k:")

здійснює побудова першого графіка суцільний чорної лінією, а другого - чорної пунктирною. Аргументи "k-" і "k:" задають стиль і колір першої і другої ліній. Тут k означає чорний колір, а дефіс або двокрапкою - суцільний або пунктирну лінію. Вікно з графіком можна закрити, натиснувши на кнопку з хрестиком у правому верхньому куті.

3. Побудова графіків функцій двох змінних

Побудова графіка функції двох змінних в MatLab на прямокутній області визначення змінних включає два попередні етапи:
1. Розбиття області визначення прямокутної сіткою.
2. Обчислення значень функції в точках перетину ліній сітки і запис їх в матрицю.
Побудуємо графік функції z(x,)= х2 + на 2 області визначення у вигляді квадрата х належить [0, 1], y - [0, 1]. Необхідно розбити квадрат рівномірної сіткою (наприклад, з кроком 0.2) і обчислити значення функцій у вузлах, позначених точками.
Зручно використовувати два двовимірних масиву х та у розмірністю шість на шість для зберігання інформації про координати вузлів. Масив х складається з однакових рядків, в яких записані координати x1, х2, ..., х6, а масив містить однакові стовпчики з y1, 2, ..., 6. Значення функції у вузлах сітки запишемо у масив z такий же розмірності (6 x 6), причому для обчислення матриці Z використовуємо вираз для функції, але з поэлементными матричними операціями. Тоді, наприклад z(3,4) як раз буде дорівнює значенню функції z(x,y)у точці (х3, 4). Для створення масивів сітки х і за координатами вузлів в MatLab передбачена функція meshgrid, для побудови графіка у вигляді каркасної поверхні - функція mesh. Наступні оператори призводять до появи на екрані з графіком функції (крапка з комою в кінці операторів не ставиться для того, щоб проконтролювати генерацію масивів):

» [X, У] = meshgrid(0:0.2:1,0:0.2:1)
X =
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
0 0.2000 0.4000 0.6000 0.8000 1.0000
y =
0 0 0 0 0 0
0.2000 0.2000 0.2000 0.2000 0.2000 0.2000
0.4000 0.4000 0.4000 0.4000 0.4000 0.4000
0.6000 0.6000 0.6000 0.6000 0.6000 0.6000
0.8000 0.8000 0.8000 0.8000 0.8000 0.8000
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000

» Z = X.^2+Y.^2

Z =
0 0.0400 0.1600 0.3600 0.6400 1.0000
0.0400 0.0800 0.2000 0.4000 0.6800 1.0400
0.1600 0.2000 0.3200 0.5200 0.8000 1.1600
0.3600 0.4000 0.5200 0.7200 1.0000 1.3600
0.6400 0.6800 0.8000 1.0000 1.2800 1.6400
1.0000 1.0400 1.1600 1.3600 1.6400 2.0000

» mesh(X,Y,Z)

Які недоліки має побудований графік? І як їх усунути? Побудований графік і новий привести в електронному звіт по лабораторній роботі.

MatLab дозволяє наносити на графік додаткову інформацію, зокрема, відповідність кольорів значенням функції. Сітка генерується за допомогою команди meshgrid, що викликається з двома аргументами. Аргументами є вектори, елементи яких відповідають сітці на прямокутній області побудови функції. Можна використовувати один аргумент, якщо область побудови функції - квадрат. Для обчислення функції слід використовувати поелементні операції.

Розглянемо основні можливості, що надаються MatLab для візуалізації функцій двох змінних, на прикладі побудови графіка функції

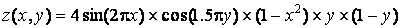
на прямокутній області визначення х належить [-1, 1], y [0, 1.]
Підготуємо матриці з координатами вузлів сітки і значеннями функції:

» [X, Y] = meshgrid(-1:0.05:1, 0:0.05:1);
» Z = 4*sin(2*пі*X).*cos(1.5*пі*Y).*(1-Х.^2).*Y.*(1-Y);

Для побудови каркасної поверхні використовується функція mesh, що викликається з трьома аргументами:

» mesh(X,Y,Z)

Колір ліній поверхні відповідає значенням функції. MatLab малює тільки видиму частину поверхні.

За допомогою команди hidden off можна зробити каркасну поверхню "прозорою", додавши приховану частина. Команда hidden on прибирає невидиму частину поверхні, повертаючи графіком колишній вигляд.

Функція surf будує каркасну поверхню графіка функції і заливає кожну клітину поверхні певним кольором, залежних від значень функції в точках, відповідних кутах клітини. У межах кожної клітини колір постійна. Подивіться результати виконання команди

» surf(X,Y,Z)

Команда shading flat дозволяє прибирати каркасні лінії. Для отримання поверхні, плавно залитої кольором, залежних від значень функції, призначена команда shading interp.
За допомогою shading faceted можна повернутися до поверхні з каркасними лініями.
3d графіки, одержувані з допомогою описаних вище команд, зручні для отримання уявлення про формі поверхні, проте за ним важко судити про значення функції. В MatLab визначена команда colorbar, яка виводить поруч з графіком стовпчик, що встановлює відповідність між кольором і значенням функції. Побудуйте за допомогою surf графік поверхні і доповніть його інформацією про кольорі.

» surf(X,Y,Z)
» colorbar

Команду colorbar можна застосовувати в поєднанні з усіма функціями, будують тривимірні об'єкти.

Користуючись кольоровий поверхнею, важко зробити висновок про значення функції в тій або іншій точці площині xy. Команди meshc або surfc дозволяють отримати більш точне уявлення про поведінку функції. Ці команди будують каркасну поверхню або залиту кольором каркасну поверхню і розміщують на площині xyлінії рівня функції (лінії постійності значень функції):

» surfc(X,Y,Z)
» colorbar

MatLab дозволяє побудувати поверхню, що складається з ліній рівня, за допомогою функції contour3. Цю функцію можна використовувати так само, як і описані вище mesh, surf, meshc і surfc з трьома аргументами. При цьому число ліній рівня вибирається автоматично. Є можливість задати четвертим аргументом у contour3 або число ліній рівня, або вектор, елементи якого рівні значень функції, які відображаються у вигляді ліній рівня. Завдання вектора (четвертого аргументу levels) зручно, коли потрібно досліджувати поведінку функції в деякій області її значень (зріз функції). Побудуйте, наприклад поверхню, що складається з ліній рівня, відповідних значень функції від 0 до 0.5 з кроком 0.01:

» levels = [0:0.01:0.5];
» contour3(X, Y, Z, levels)
» colorbar

4. Побудова контурних графіків функцій двох змінних

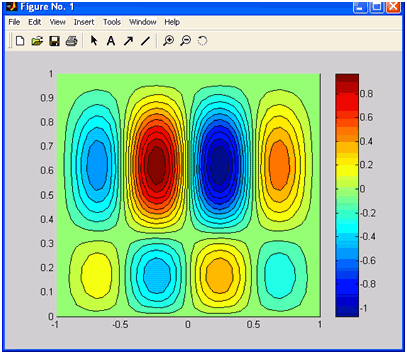
MatLab надає можливість отримувати різні типи контурних графіків за допомогою функцій contour і contourf. Розглянемо їх можливості на прикладі функції

.

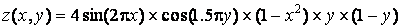Використання contour з трьома аргументами

» contour(X,Y,Z)

призводить до графіку, на якому показано лінії рівня на площині xy, але без вказівки числових значень на них. Такий графік є малоінформативним, він не дозволяє дізнатися значення функції на кожній з ліній рівня. Використання команди colorbar також не дозволить точно визначити значення функції. Кожну лінію рівня можна забезпечити значенням, яке приймає на ній досліджувана функція, за допомогою певної в MatLab функції clabel. Функція clabel викликається з двома аргументами: матрицею, що містить інформацію про лініях рівня і вказівником на графік, на якому слід нанести розмітку. Користувачеві не потрібно самому створювати аргументи clabel. Функція contour, викликана з двома вихідними параметрами, не тільки будує лінії рівня, але і знаходить необхідні для clabel параметри. Використовуйте contour з вихідними аргументами CMatr і h (в масиві CMatr міститься інформація про лініях рівня, а в масиві h - покажчики). Завершіть виклик contour крапкою з комою для придушення виводу на екран значень вихідних параметрів і нанесіть на графік сітку:

» [CMatr, h] = contour(X, Y, Z);
» clabel(CMatr, h)
» grid on

Додатковим аргументом функції contour (так само, як і contour3, описаної вище) може бути або число ліній рівня, або вектор, що містить значення функції, для яких потрібно побудувати лінії рівня.
Наочну інформацію про зміну функції дає заливка прямокутника на площині xyкольором, залежних від значення функції в точках площині. Для побудови таких графіків призначена функція contourf, використання якої не відрізняється від застосування contour. У наступному прикладі виводиться графік, який складається з двадцяти ліній рівня, а проміжки між ними заповнені квітами, відповідними значеннями досліджуваної функції:

» contourf(X, Y, Z, 20)
» colorbar

5. Оформлення графіків функцій

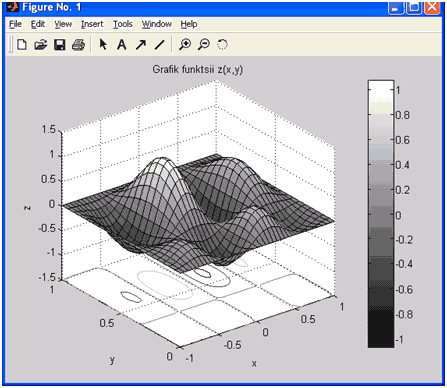
Простим і ефективним способом зміни колірного оформлення графіка є установка колірної палітри за допомогою функції colormap. Наступний приклад демонструє підготовку графіка функції для друку на монохромному принтері, використовуючи палітру gray.

» surfc(X, Y, Z)
»colorbar
» colormap(gray)
» title"(Графік функції z(x,y)")
» xlabel("x")
» ylabel("у")
» zlabel("z")

Зверніть увагу, що команда colormap(gray) змінює палітру графічного вікна, тобто наступні графіки будуть виводитися у цьому вікні також в сірих тонах. Для відновлення первісного значення панелі слід застосувати команду colormap("default"). Кольорові панелі, доступні в MatLab, наведено в табл. 2.

Таблиця 2

6. Висновок декількох графіків на одні осі

Для відображення декількох графіків функцій однієї змінної на одних осях використовувалися можливості функцій plot, plotyy, semilogx, semilogy, loglog. Вони дозволяють виводити графіки декількох функцій, задаючи відповідні векторні аргументи парами, наприклад plot(x,f,x,g). Однак для об'єднання тривимірних графіків їх використовувати не можна. Для об'єднання таких графіків призначена команда hold on, яку потрібно поставити перед побудовою графіка. У наступному прикладі об'єднання двох графіків (площині і конуса) призводить до їх перетину. Конус задається параметрично наступними залежностями:

, , , .

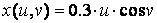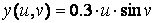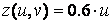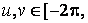
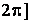Для графічного відображення конуса спочатку необхідно згенерувати за допомогою двокрапки вектор-стовпчик і вектор-рядок, що містять значення параметрів на заданому інтервалі (важливо, що u - вектор-стовпчик, а v-вектор-рядок):

» u = [-2*pi:0.1*pi:2*pi]";
» v = [-2*pi:0.1*pi:2*pi];

Далі формуються матриці X, Y, що містять значення функцій 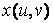і 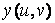у точках, відповідних значень параметрів. Формування матриць виконується за допомогою зовнішнього твори векторів.

Примітка 2

Зовнішнім твором векторів 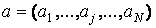, 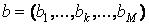називається матриця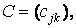 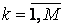розміру N x M, елементи якої обчислюються за формулою .
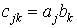пВектор вектор-стовпцем ів MatLab представляється у вигляді двомiрного масива розміру N на один. Вектор-стовпчик b при транспонировании переходить в вектор-рядок розміру один на М. Вектор-стовпчик і вектор-рядок є матриці, у яких один з розмірів дорівнює одиниці. Фактично, = abT, де множення відбувається за правилом матричного твори. Для обчислення матричного твори в MatLab використовується оператор "зірочка". Визначимо зовнішнє твір для двох векторів:

» a= [1;2;3];
» b= [5;6;7];
» C = a*b"
C =
5 6 7
10 12 14
15 18 21

Сформуємо матриці X,Y, необхідні для графічного відображення конуса:

» X = 0.3*u*cos(v);
» Y = 0.3*u*sin(v);

Матриця Z повинна бути того ж розміру, що і матриці X іY. Крім того, вона повинна містити значення, відповідні значень параметрів. Якщо б у функцію 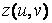входило твір і і v, то матрицю Z можна було заповнити аналогічно матриць Xі Yза допомогою зовнішнього твори. З іншого боку, функцію z(u,v)можна представити у вигляді 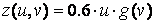, де 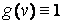. Тому для обчислення Zможна застосувати зовнішнє добуток векторів 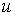і 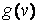, де вектор-рядок має ту ж розміри, що v, але складається з одиниць:

» Z = 0.6*u*ones(size(v));

Всі необхідні матриці для відображення конуса створені. Завдання площині виконується наступним чином:

» [X,Y] = meshgrid(-2:0.1:2);
» Z = 0.5*X+0.4*Y;

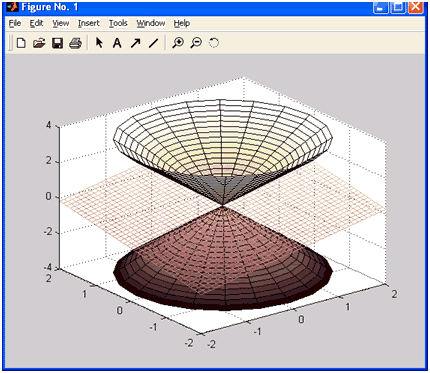
Тепер не складно записати і повну послідовність команд для побудови пересічних конуса і площині:

» u = [-2*pi:0.1*pi:2*pi]";
» v = [-2*pi:0.1*pi:2*pi];
» X = 0.3*u*cos(v);
» Y = 0.3*u*sin(v);
» Z = 0.6*u*ones(size(v));
» surf(X, Y, Z)
» [X,Y] = meshgrid(-2:0.1:2);
» Z = 0.5*X+0.4*Y;
» hold on
» mesh(X, Y, Z)
» hidden off

Команда hidden off застосована для того, щоб показати частина конуса, що знаходиться під площиною.
Зверніть увагу, що команда hold on поширюється на всі наступні висновки графіків в поточне вікно. Для розміщення графіків у нових вікнах слід виконати команду hold off. Команда hold on може застосовуватися і для розташування декількох графіків функцій однієї змінної, наприклад,

» plot(x,f,х,g)

еквівалентно послідовності

» plot(х,f)
» hold on
» plot(x,g)

Результати роботи, отримані мною: