1. Різні способи введення матриць в пакеті MatLab
Вводити невеликі за розміром матриці зручно прямо з командного рядка. Введіть матрицю розміром два на три

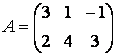 .
.
Для зберігання матриці використовуйте двовимірний масив з ім'ям A. При введенні врахуйте, що матрицю можна розглядати як вектор-стовпчик з двох елементів, кожен з яких є вектор-рядком довжиною три, отже, рядки при наборі відокремлюються крапкою з комою:
» А= [3 1 -1; 2 4 3]
А =
3 1 -1
2 4 3
Для вивчення найпростіших операцій над матрицями наведемо ще кілька прикладів. Розглянемо інші способи введення. Введіть квадратну матрицю розміру три так, як описано нижче:
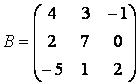 .
.
Почніть набирати в командному рядку
» = [4 3 -1
Натисніть клавішу <Enter>. Зверніть увагу, що пакет нічого не рахував. Курсор блимає на наступному рядку без символу ». Продовжуйте введення матриці по рядках, натискаючи наприкінці кожного рядка <Enter>. Останній рядок завершіть закриває квадратної дужкою, виходить:
2 7 0
-5 1 2]
B =
4 3 -1
2 7 0
-5 1 2
Ще один спосіб введення матриць полягає в тому, що матрицю можна трактувати як вектор-рядок, кожен елемент якої є вектор-стовпцем. Наприклад, матрицю два на три
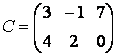
можна ввести за допомогою команди:
= [[3; 4] [-1; 2] [7; 0]]
С =
3 -1 7
4 2 0
Подивіться змінні середовища, набравши в командному рядку whos:
А 2x3 48 double array
3x3 72 double array
З 2x3 48 double array
Отже, в робочому середовищі міститься три матриці, дві прямокутні і одна квадратна.
2. Звернення до елементів матриць в пакеті MatLab
Доступ до елементів матриць здійснюється за допомогою двох індексів номерів рядка та стовпчика, укладених в дужки, наприклад
» З(2, 3)
ans =
0
Елементи матриць можуть входити до складу виразів:
» (З 1, 1) + (2, 2) + (2, 3)
ans =
5
Розташування елементів матриці в пам'яті комп'ютера визначає ще один спосіб звернення до них. Матриця розміру m n зберігається у вигляді вектора довжини mn, в якому елементи матриці розташовані один за одним по стовпцях
[А(1,1) А(2,1) ... А(m,1) ... А(1,n) А(2,n) ... А(m,n)].
Для доступу до елементів матриці можна використовувати один індекс задає порядковий номер елемента матриці у векторі.
Матриця , визначена у попередньому підрозділі, міститься у векторі
[C(1,1) C(2,1) C(1,2) З(2,2) З(1,3) З(2,3)],
який має шість компонент. Доступ до елементів матриці здійснюється наступним чином:
» З(1)
ans =
3
» З(5)
ans =
7
3. Операції над матрицями в пакеті MatLab: додавання, віднімання, множення, транспонування і піднесення до степеня
При використанні матричних операцій слід пам'ятати, що для додавання або віднімання матриці повинні бути одного розміру, а при перемножении кількість стовпчиків першої матриці повинно дорівнювати кількості рядків другий матриці. Додавання і віднімання матриць, так само як чисел і векторів, здійснюється за допомогою знаків плюс і мінус. Знайдіть суму і різниця матриць З і , визначених вище:
» S = А+С
S =
6 0 6
6 6 3
» R = - А
R =
0 -2 8
2 -3 -2
Слідкуйте за збігом розмірності, інакше отримаєте повідомлення про помилку:
» S = А+В
??? Error using ==> ±
Matrix dimensions must agree.
Для множення матриць призначена зірочка:
» Р = *
P =
-25 9 11
20 26 -4
Множення матриці на число теж здійснюється за допомогою зірочки, причому множити на число можна як справа, так і зліва:
» Р = *3
Р =
9 3 -3
6 12 -3
» Р = 3*А
Р =
9 3 -3
6 12 9
Транспонування матриці, так само як і вектора, здійснюється за допомогою .", а символ " означає комплексне товариш. Для речових матриць ці операції призводять до однакових результатів:
»"
ans =
4 2 -5
3 7 1
-1 0 2
» В".
ans =
4 2 -5
3 7 1
-1 0 2
Примітка 1
Якщо матриця 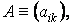
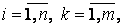 є довільна матриця розміру n m, то матриця, перенести по відношенню до Є матриця розміру m n:
є довільна матриця розміру n m, то матриця, перенести по відношенню до Є матриця розміру m n: 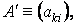
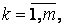
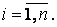 Таким чином, рядки матриці
Таким чином, рядки матриці 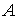 стають стовпцями матриці
стають стовпцями матриці 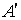 , а стовпці матриці
, а стовпці матриці 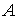 стають рядками матриці
стають рядками матриці  .
.
пКомплексно-сполучена матриця виходить з вихідної в два етапи: виконується транспонування вихідної матриці, а потім всі комплексні числа замінюються на комплексно-зв'язані.
Товариш і транспонування матриць, що містять комплексні числа, приведуть до створення різних матриць:
»K= [l-i, 2+3i; 3-5i, l-9i]
К = 1.0000 - 1.0000i 2.0000 + 3.0000i
3.0000 - 5.0000i 1.0000 - 9.0000i
»K"
ans =
1.0000 + 1.0000i 3.0000 + 5.0000i
2.0000 - 3.0000i 1.0000 + 9.0000i
» K."
ans =
1.0000 - 1.0000i 3.0000 - 5.0000i
2.0000 + 3.0000i 1.0000 - 9.0000i
Примітка 2
При введенні вектор-рядків їх елементи можна поділити або пробілами, або комами. При введенні матриці застосовані коми для більш наочного поділу комплексних чисел в рядку.
Зведення квадратної матриці в цілу ступінь виробляється з використанням оператора ^:
» В2 = ^2
B2 =
27 32 -6
22 55 -2
-28 -6 9
Перевірте отриманий результат, помноживши матрицю на саму себе.
Переконайтеся, що ви освоїли найпростіші операції з матрицями в MatLab. Знайдіть значення наступного виразу
( + ) 3 (A-З)Т.
Врахуйте пріоритет операцій, спочатку виконується транспонування, потім піднесення до степеня, потім множення, а додавання і віднімання проводяться в останню чергу.
»(А+С)*^3*(А)-З"
ans =
1848 1914
10290 3612
4. Множення матриць і векторів
Вектор-стовпчик або вектор-рядок в MatLab є матрицями, у яких один з розмірів дорівнює одиниці, тому всі вищеописані операції застосовуються для множення матриці на вектор-стовпчик або вектор-рядки на матрицю. Наприклад, вираз

можна здійснити наступним чином:
» a = [1 3 -2];
» B= [2 0 1; -4 8 -1; 0 9 2];
» c= [-8; 3; 4];
» a*B*c
ans =
74
5. Блокові матриці
Дуже часто в додатках виникають так звані блокові матриці, тобто матриці, складені з непересічних підматриць (блоків). Розглянемо спочатку конструювання блочних матриць. Введіть матриці: 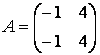 ,
, 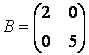 ,
, 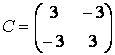 ,
, 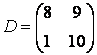 та створіть з них блочну матрицю
та створіть з них блочну матрицю 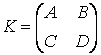 .
.
Враховуючи, що матриця складається з двох рядків, у першому рядку матриці і B, а в другій - і D, блочну матрицю можна сформувати наступним чином:
» К = [А В; D]
K =
-1 4 2 0
-1 4 0 5
3 -3 8 9
-3 3 1 10
Блочну матрицю можна отримати і іншим способом, якщо вважати, що матриця складається з двох стовпчиків, в першому - матриці і С а в другому - і D:
Зворотного завданням до конструювання блочних матриць є завдання виділення блоків. Виділення блоків матриць індексацією здійснюється за допомогою двокрапки. Введіть матрицю
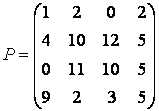
і потім виділіть подматрицу з елементами 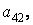
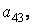
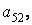
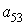 , задавши номери рядків і стовпців за допомогою двокрапки:
, задавши номери рядків і стовпців за допомогою двокрапки:
»Р1 = P(2:3,2:3)
Р1 =
10 12
11 10
Для виділення з матриці стовпчика або рядка (тобто масиву, у якого один з розмірів дорівнює одиниці) слід в якості одного з індексів використовувати номер стовпчика або рядка матриці, а інший індекс замінити двокрапкою без вказівки меж. Наприклад, запишіть другий рядок матриці Р у вектор р
»p = P(2, :)
p =
4 10 12 5
При виділенні блоку до кінця матриці можна не вказувати її розміри, а використовувати елемент end:
»p = P(2, 2:end)
p =
10 12 5
6. Видалення рядків і стовпців
В MatLab парні квадратні дужки [ ] позначають порожній масив, який, зокрема, дозволяє видаляти рядки та стовпці матриці. Для видалення рядка слід присвоїти їй порожній масив. Видаліть, наприклад, перший рядок квадратної матриці:
» М = [2 0 3
1 1 4
6 1 3];
» M(1,:)=[];
» M
M =
1 1 4
6 1 3
Зверніть увагу на відповідну зміну розмірів масиву, яке можна перевірити за допомогою size:
» size(M)
ans =
2 3
Аналогічним чином видаляються і стовпці. Для видалення декількох що йдуть підряд стовпчиків або рядків) їм потрібно надати порожній масив. Видаліть другий і третій стовпчик у масиві M
» М(:, 2:3) = []
M =
1
6
Індексація суттєво економить час при введенні матриць, що мають певну структуру.
7. Заповнення матриць за допомогою індексації
Вище було описано кілька способів введення матриць в MatLab. Однак часто буває простіше згенерувати матрицю, ніж вводити її, особливо якщо вона має простий структурою. Розглянемо приклад такої матриці:
 .
.
Генерація матриці Т здійснюється в три етапи:
1. Створення масиву T розміру на п " ять, що складається з нулів.
2. Заповнення першого рядка одиницями.
3. Заповнення частини останнього рядка мінус одиницями до останнього елемента.
Відповідні команди MatLab наведені нижче.
» A(1:5, 1:5) = 0
A=
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
» A(1, :) = 1
A=
1 1 1 1 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
» A(end, 3:end) = -1
A=
1 1 1 1 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 -1 -1 -1
Створення деяких спеціальних матриць в MatLab здійснюється за допомогою вбудованих функцій.
8. Створення матриць спеціального виду
Заповнення прямокутної матриці нулями проводиться вбудованою функцією zeros, аргументами якої є число рядків і стовпців матриці:
» A = zeros(3, 6)
A =
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
Один аргумент для функції zeros призводить до утворення квадратної матриці заданого розміру:
» A = zeros(3)
A =
0 0 0
0 0 0
0 0 0
Одинична матриця ініціалізується за допомогою функції eye:
» I = eye(4)
I=
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Функція eye з двома аргументами створює прямокутну матрицю, у якої на головної діагоналі стоять одиниці, а інші елементи дорівнюють нулю:
» I = eye(4, 8)
I =
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
Матриця, що складається з одиниць, утворюється в результаті виклику функції
ones:
» E = ones(3, 7)
E =
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
Використання одного аргументу в ones призводить до створення квадратної матриці, що складається з одиниць.
MatLab надає можливість заповнення матриць випадковими елементами. Результатом функції rand є матриця чисел, розподілених випадковим чином між нулем і одиницею, а функції randn - матриця чисел, розподілених по нормальному закону:
» R = rand(3, 5)
R =
0.9501 0.4860 0.4565 0.4447 0.9218
0.2311 0.8913 0.0185 0.6154 0.7382
0.6068 0.7621 0.8214 0.7919 0.1763
Один аргумент функцій rand і randn призводить до формування квадратних матриць:
Часто виникає необхідність створення діагональних матриць, тобто матриць, у яких все недиагональные елементи дорівнюють нулю. Функція diag формує діагональну матрицю з вектор-стовпчика або вектор-рядки, розташовуючи їх елементи по діагоналі матриці:
» d= [1; 2; 3; 4];
» D = diag(d)
D =
1 0 0 0
0 2 0 0
0 0 3 0
0 0 0 4
Функція diag служить і для виділення діагоналі матриці в вектор, наприклад
» A= [10 1 2; 1 20 3; 2 3 30];
» d = diag(A)
d =
10
20
30
9. Поелементні операції з матрицями
Оскільки вектори та матриці зберігаються в двовимірних масивах, то застосування математичних функцій до матриць і поелементні операції проводяться так само, як для векторів.
Введіть дві матриці
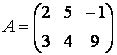 ,
, 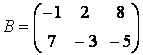 .
.
Множення кожного елемента однієї матриці на відповідний елемент інший проводиться за допомогою оператора .*:
= *В
С =
-2 10 -8
21 -12 -45
Для розподілу елементів першої матриці на відповідні елементи другий використовується оператор ./, а для розподілу елементів другий матриці на відповідні елементи першої служить .\:
» R1 = А.В1/
R1 =
-2.0000 2.5000-0.1250
0.4286-1.3333-1.8000
» R2 = А.\В1
R2 =
-0.5000 0.4000-8.0000
2.3333-0.7500-0.5556
Поелементне зведення у ступінь здійснюється за допомогою оператора .^. Показник ступеня може бути числом чи матрицею того ж розміру, що і матриця, вчинений у ступінь. У другому випадку елементи першої матриці зводяться в ступеня, рівні елементів другий матриці.
10. Візуалізація матриць
Матриці з досить великою кількістю нулів називаються розрідженими. Часто необхідно знати, де розташовані ненульові елементи, тобто отримати так званий шаблон матриці. Для цього в MatLab є функція spy. Подивимося шаблон матриці G
 .
.
» spy(G)
Після виконання команди spy на екрані з'являється графічне вікно Figure No. 1. На вертикальної і горизонтальної вісі відкладені номери рядків і стовпців. Ненульові елементи позначені маркерами, внизу графічного вікна вказано кількість ненульових елементів (nz = 19).
Наочну інформацію про співвідношення величин елементів матриці дає функція imagesc, яка інтерпретує матрицю як прямокутне зображення. Кожен елемент матриці представляється у вигляді квадратики, колір якого відповідає величині елемента. Для того щоб дізнатися відповідність кольору і розміру елемента слід використовувати команду colorbar, що виводить поруч із зображенням матриці шкалу кольору (Insert (в графічному вікні Figure &No.nbsp; 1), colorbar). Нарешті, для друку на монохромному принтері зручно отримати зображення у відтінках сірого кольору, використовуючи команду colormap(gray) (Edit (в графічному вікні Figure &No.nbsp;1), Colormap, Colormap Editor, Tools, gray). Ми будемо працювати з матрицею G. Набирайте команди, вказані нижче, і стежте за станом графічного вікна:
» imagesc(G)
» colorbar
» colormap(gray)
У результаті виходить наочне уявлення матриці.


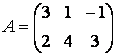 .
.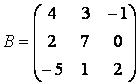 .
.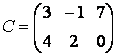

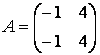 ,
, 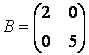 ,
, 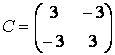 ,
, 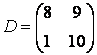 та створіть з них блочну матрицю
та створіть з них блочну матрицю 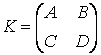 .
. 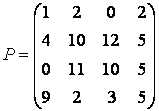
 .
.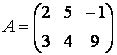 ,
, 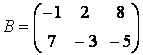 .
. .
.