I, II. Додавання. Віднімання.
а) 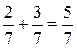 ; б)
; б) 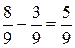 .
.
Додавання й віднімання дробів з однаковими знаменниками (сформулювати правило).
в) 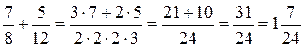 .
.
Знаменники дробів розкладуються на множники 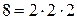 і
і 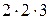 .
.
Додавання й віднімання дробів з різними знаменниками (сформулювати правило).
Правило. Щоб скласти (відняти дроби з різними знаменниками), потрібно:
1). Знайти їх загальний знаменник (для цього знаменники дробів розкласти на множники, виписати множники одного з них і дописати в добуток відсутні множники іншого);
2). Знайти додаткові множники (для цього загальний знаменник розділити на знаменник даного дробу);
3). Додаткові множники помножити на відповідні чисельники й провести додавання (віднімання).
г) 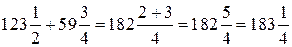 .
.
Правило. Щоб скласти мішані числа, потрібно скласти їхні цілі частини, а потім дробові за попереднім правилом.
Звернути увагу на те, як потрібно зробити, якщо при відніманні мішаних чисел здійснити віднімання дробових частин неможливо
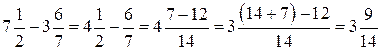 .
.
А також сформулювати правило віднімання дробу із цілого числа.
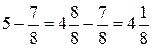 .
.
III. Множення дробів.
а) 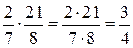 .
.
Правило. Щоб помножити дріб на дріб, потрібно перемножити їхні чисельники й знаменники. Перший добуток поставити в чисельник, а другий – у знаменник.
Звернути увагу на те, що потрібно перевірити, чи не можна скоротити дроби перед тим, як їх множити.
б) 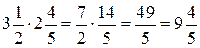 .
.
Правило. Щоб перемножити мішані числа, треба їх спочатку перетворити в неправильні дроби, а потім зробити дію множення по попередньому правилу. Звернути увагу на те, що якщо потрібно помножити число на дріб (або дріб на число), то ціле число представляємо у вигляді дробу зі знаменником один, а потім робимо дію.
IV. Ділення дробів.
Означення. Два числа називаються взаємно зворотними, якщо їхній добуток дорівнює одиниці, 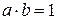 ,
, 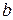 і
і 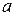 – зворотні.
– зворотні.
Числу 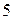 зворотне
зворотне 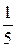 , а числу
, а числу 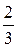 зворотне –
зворотне – 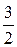 .
.
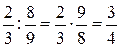 .
.
Правило. Щоб дріб розділити на дріб, потрібно перший дріб помножити на дріб, зворотний до другого.


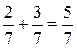 ; б)
; б) 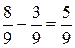 .
.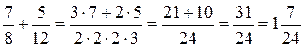 .
.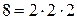 і
і 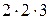 .
.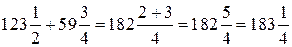 .
.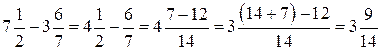 .
.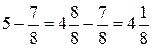 .
.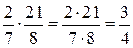 .
.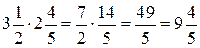 .
.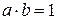 ,
, 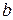 і
і 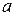 – зворотні.
– зворотні.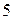 зворотне
зворотне 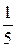 , а числу
, а числу 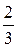 зворотне –
зворотне – 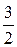 .
.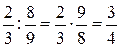 .
.