Заміна: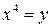 
, тоді 
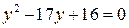, його розв’язки 
; 
.
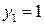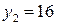Повертаючись до змінної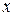 
, маємо сукупність рівнянь:
а)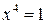 
; 
.
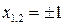б)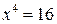 
; 
.
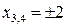Відповідь: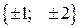 
.
2) Симетричні рівняння четвертого степеня:
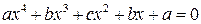; (2)
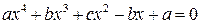, (3)
де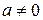 
.
Оскільки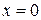 
не є коренем цих рівнянь, то поділимо рівняння на 
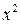, маємо:
;
,
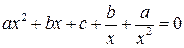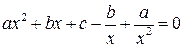або
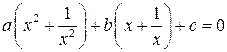; (2а)
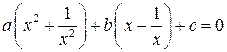. (3а)
Для рівняння (2а) заміна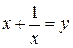 
, тоді 
.
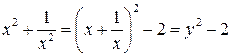Для рівняння (3а)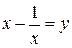 
, тоді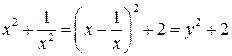 
Внаслідок цього задані рівняння зводяться до квадратних.
Приклад 2.Розв’язати рівняння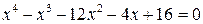 
.
