Означення границі функції. Геометричні зображення. Границя функції зліва то справа. Границя функції на нескінченності.

Точка х₀ називається граничною точкою множини Е, якщо в будь-якому хоколі точки x₀ є точки множини Е відмінні від точки x₀. Нехай функція y=f(x) означена на множині Е і x₀ – гранична точка цієї множини. Число а називається границею функції y=f(x) у точці x₀ чи при х, яке прямує до x₀, якщо таке, що для всіх х, які задовольняють нерівності 0<|x-x₀|<d, виконується нерівність |f(x)-a|<e. Це означення границі функції за Коші.

Число а називають границею функції f(x) у точці x₀, якщо для будь-якої послідовності {x_n}, x_n є E, що скорочується до x₀, відповідна послідовність значень функції {f(x_n)} збігається з числом а. Це означення границі функції за Гейне.

Число А є границею функції f(x) зліва (лівою границею), якщо для будь-якого числа e<0 існує d=d(e)>0 таке, що при x є (x₀-d; х₀) виконується нерівність

|f(x)-A|<e

Число B є границею функції f(x) справа (правою границею), якщо для як завгодно малого значення e>0 знайдеться d=d(e)>0 таке, що для всіх x з проміжку x є (x₀; х₀+d) виконується нерівність |f(x)-В|<e

Ліва і права границі називаються одностороннніми границями.

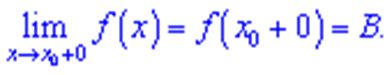
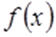Число b називається границею функції при 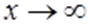, якщо для будь-якого як завгодно малого числа 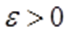існує таке додатне число N, що для всіх x, які задовольняють нерівність 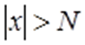, виконується нерівність

.

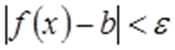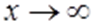Скорочено означення границі при можна записати так:

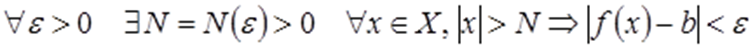Якщо при цьому елементи 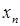послідовності 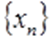додатні (від’ємні), то пишуть так: