Нехай задано дугу 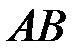 графіка функції
графіка функції 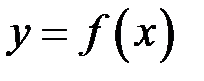 , яку будемо вважати
, яку будемо вважати
неперервною та неперервно диференційовною на відрізку 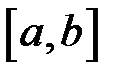 (рис. 15)
(рис. 15)
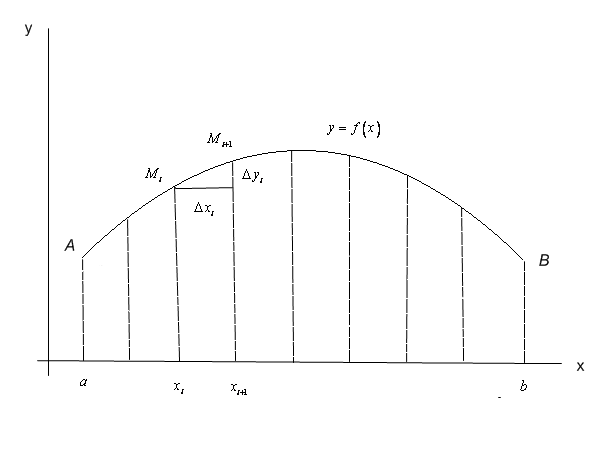
Рис. 15.
Розіб’ємо відрізок 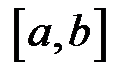 довільно обраними точками ділення на частинні :
довільно обраними точками ділення на частинні :
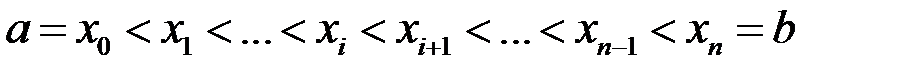 .
.
Відмітимо на графіку функції точки 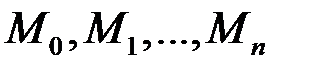 з абсцисами відповідно
з абсцисами відповідно 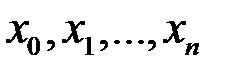 . З’єднаємо їх відрізками прямих ліній. Дістанемо ламану лінію
. З’єднаємо їх відрізками прямих ліній. Дістанемо ламану лінію 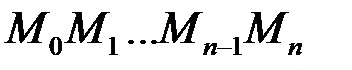 , яку вписано в дугу
, яку вписано в дугу 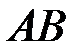 . Позначимо периметр цієї ламаної через
. Позначимо периметр цієї ламаної через 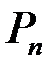 .
.
Означення. Якщо існує і не залежить від способу вписування ламаної скінченна границя периметра цієї ламаної, коли найбільший її відрізок прямує до нуля, то крива 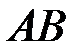 називається спрямною, а величина цієї границі називається довжиною дуги і позначається
називається спрямною, а величина цієї границі називається довжиною дуги і позначається
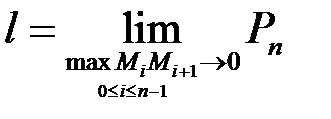 . (15.1)
. (15.1)
Позначимо 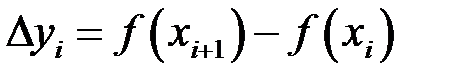 ,
, 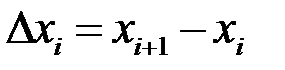 ,
, 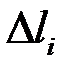 – довжину відрізка
– довжину відрізка 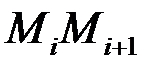 . Очевидно, що
. Очевидно, що
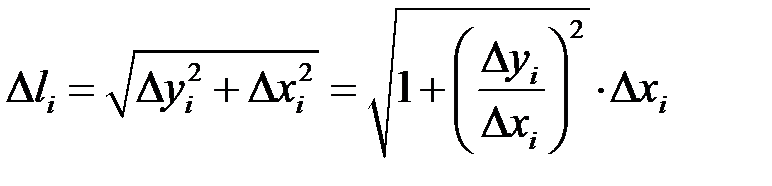 .
.
За теоремою Лагранжа на інтервалі 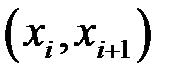 існує точка
існує точка 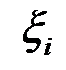 така, що
така, що
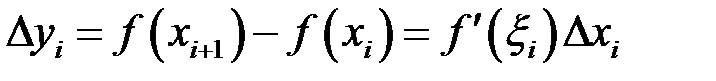 .
.
Тоді
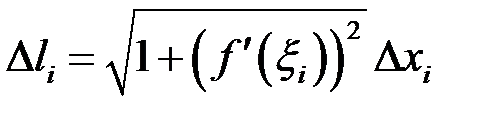 ,
,
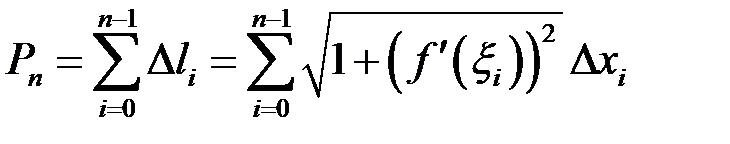 .
.
Це є інтегральна сума для функції 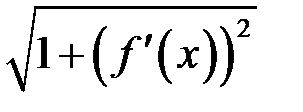 . Оскільки
. Оскільки 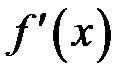 неперервна, функція
неперервна, функція 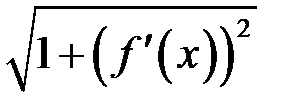 також неперервна, і тоді існує границя (15.1):
також неперервна, і тоді існує границя (15.1):
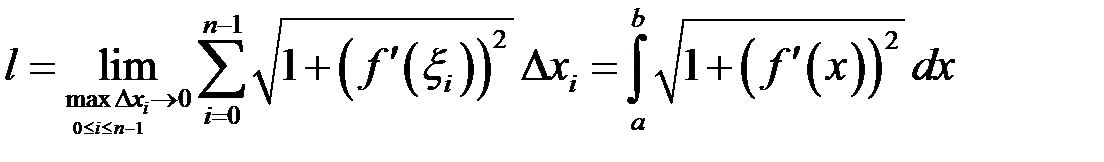 .
.
Отже дістали формулу:
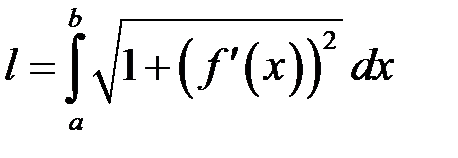 . (15.2)
. (15.2)
Приклад 1. Обчислити довжину дуги напівкубічної параболи 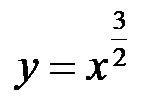 на відрізку
на відрізку 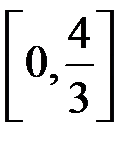 (рис. 16).
(рис. 16).
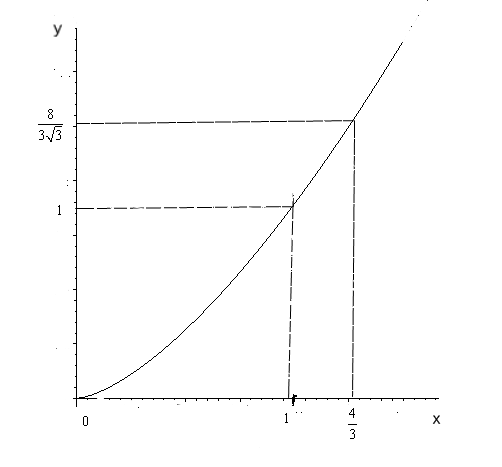
Рис. 16.
Маємо: 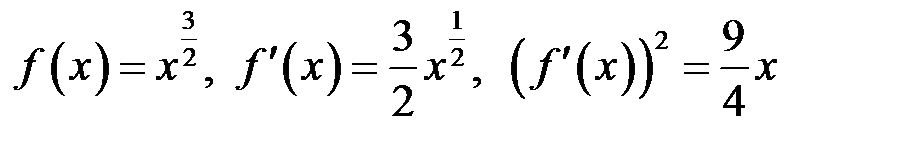 . Отже
. Отже
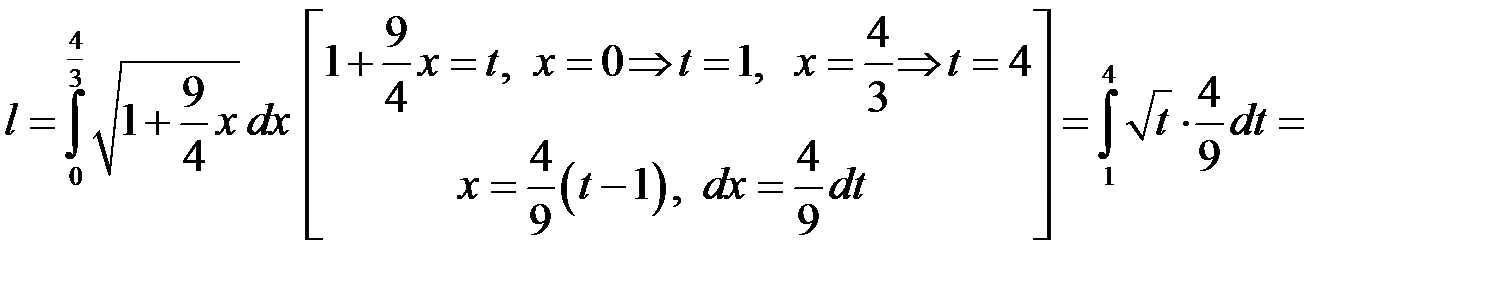
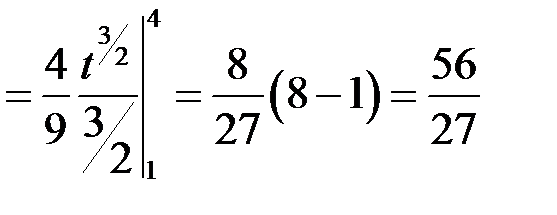 .
.
Приклад 2. Обчислити довжину графіка функції 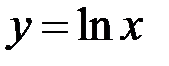 на відрізку
на відрізку 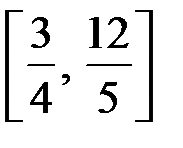 .
.
Маємо: 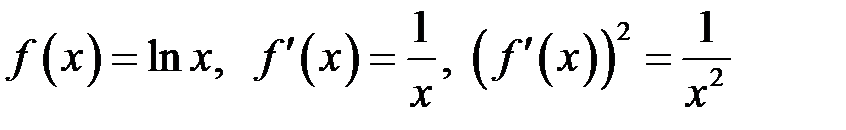 . Отже
. Отже
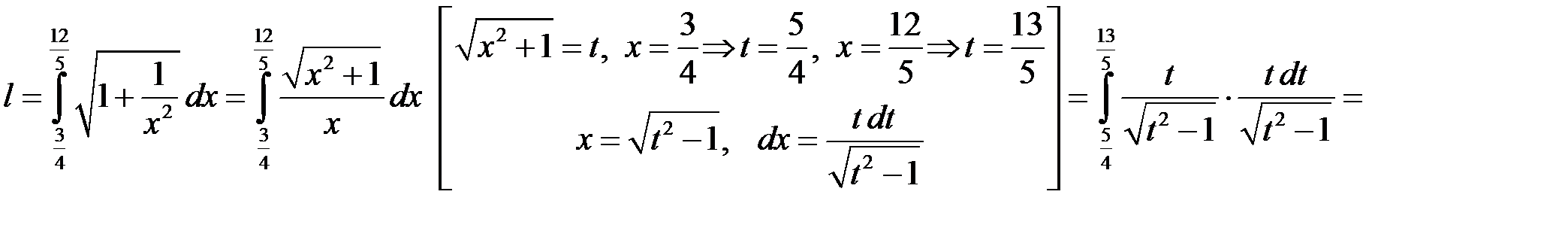
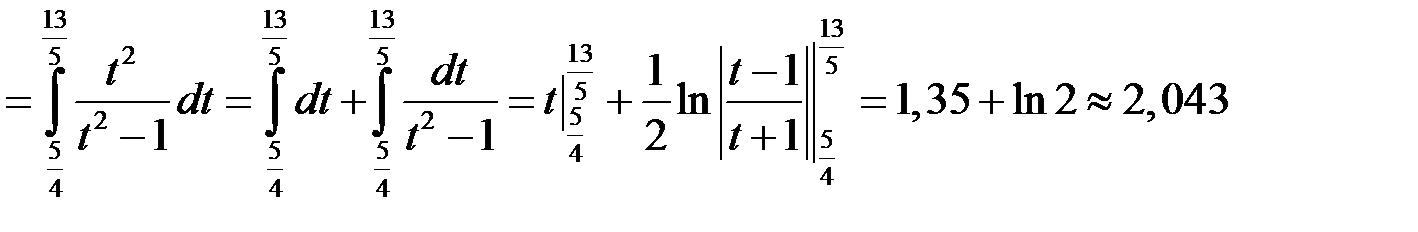 .
.
Якщо криву 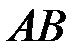 задано параметрично:
задано параметрично: 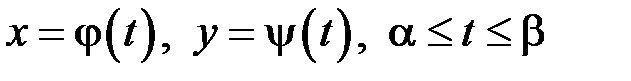 , де
, де 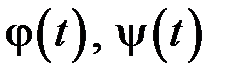 – неперервно диференційовні на проміжку
– неперервно диференційовні на проміжку 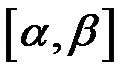 функції, то:
функції, то:
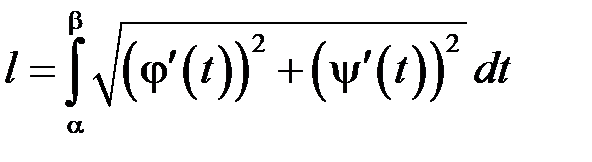 . (15.3)
. (15.3)
Приклад. Обчислити довжину однієї арки циклоїди, яка має параметричні рівняння:
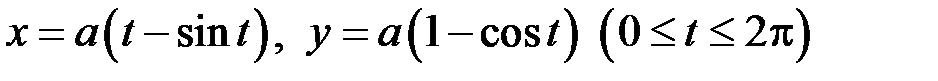 .
.
Циклоїда – це лінія, яку описує точка на колі радіуса 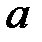 , яке котиться вздовж прямої лінії. У якості параметра
, яке котиться вздовж прямої лінії. У якості параметра 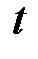 виступає кут поворота кола (рис. 17).
виступає кут поворота кола (рис. 17).
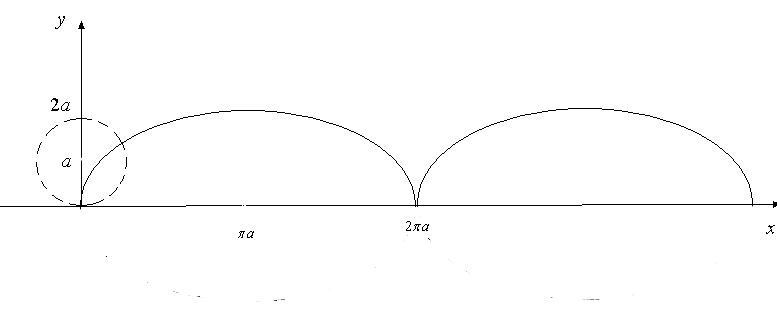
Рис. 17.
За формулою (15.3) маємо:
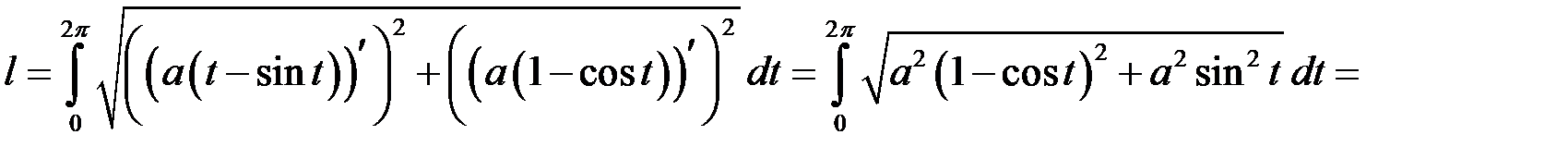
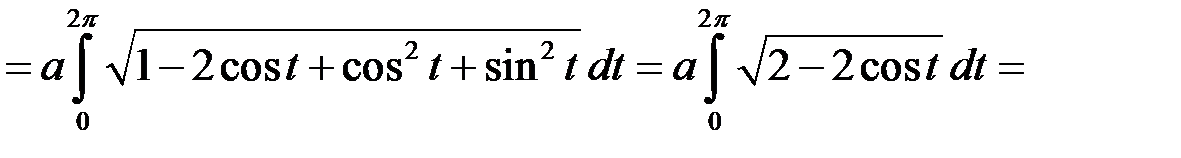
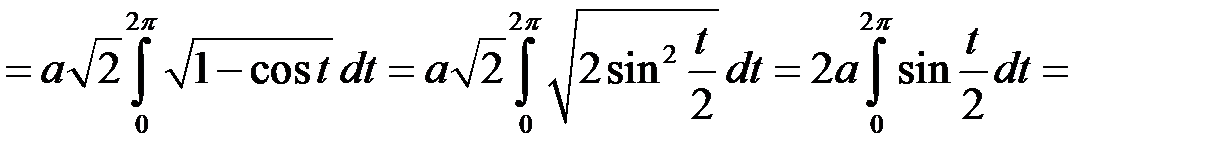
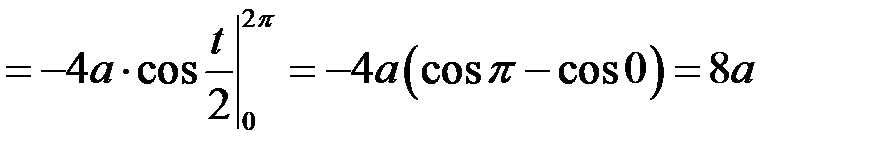 .
.
Якщо криву задано у полярній системі координат 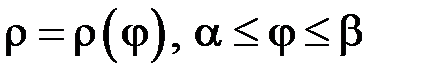 , де
, де 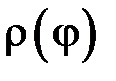 – неперервно диференційовна на
– неперервно диференційовна на 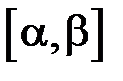 функція, то можна довести, що
функція, то можна довести, що
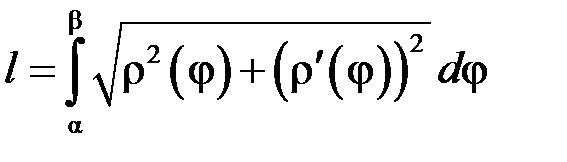 . (15.4)
. (15.4)
Приклад. Обчислити довжину дуги логарифмічної спіралі 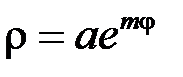
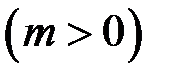 за умовою
за умовою 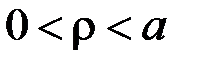 (рис. 18).
(рис. 18).
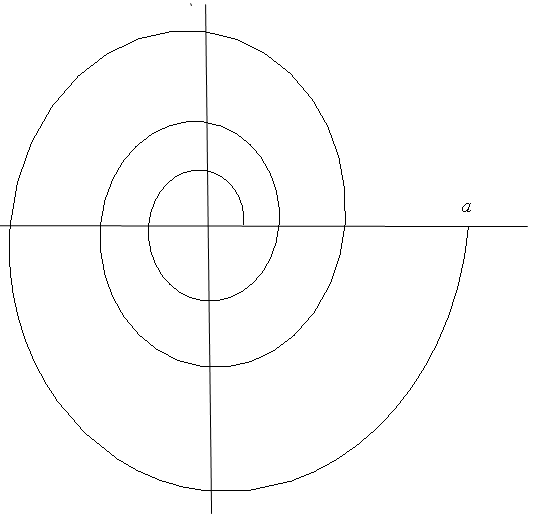
Рис. 18.
Внаслідок того, що 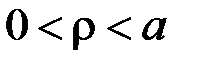 , дістаємо:
, дістаємо: 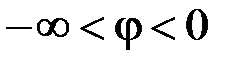 , отже за формулою (15.4) матимемо:
, отже за формулою (15.4) матимемо:
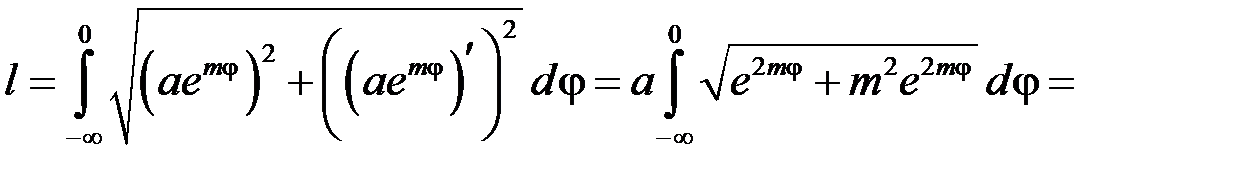
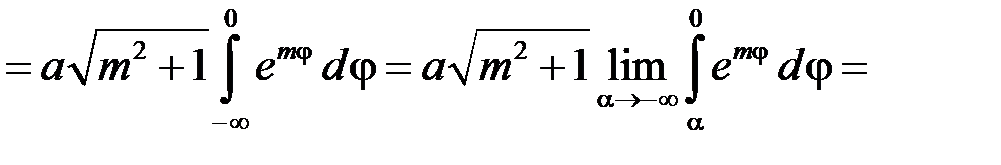
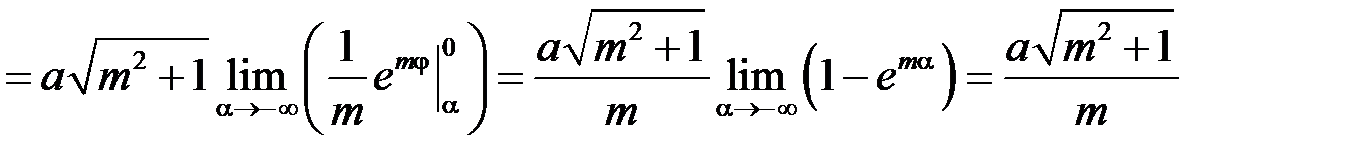
через те, що 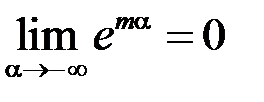 . Зауважимо, що інтеграл, який тут виникає – невласний 1-го роду.
. Зауважимо, що інтеграл, який тут виникає – невласний 1-го роду.


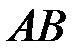 графіка функції
графіка функції 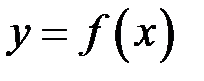 , яку будемо вважати
, яку будемо вважати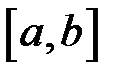 (рис. 15)
(рис. 15)
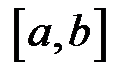 довільно обраними точками ділення на частинні :
довільно обраними точками ділення на частинні :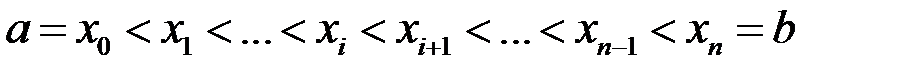 .
.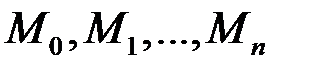 з абсцисами відповідно
з абсцисами відповідно 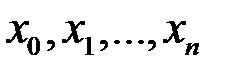 . З’єднаємо їх відрізками прямих ліній. Дістанемо ламану лінію
. З’єднаємо їх відрізками прямих ліній. Дістанемо ламану лінію 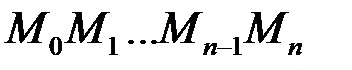 , яку вписано в дугу
, яку вписано в дугу 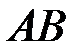 . Позначимо периметр цієї ламаної через
. Позначимо периметр цієї ламаної через 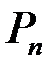 .
.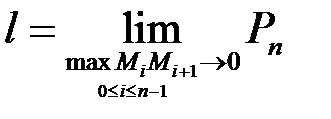 . (15.1)
. (15.1)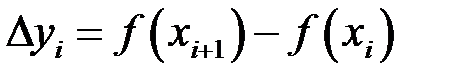 ,
, 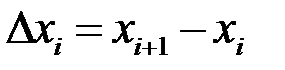 ,
, 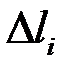 – довжину відрізка
– довжину відрізка 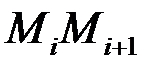 . Очевидно, що
. Очевидно, що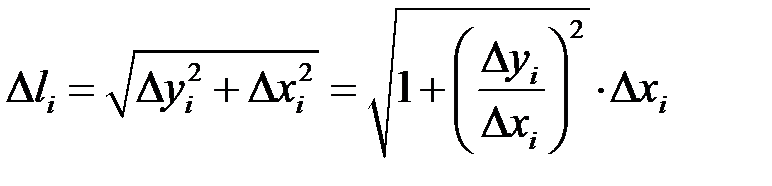 .
.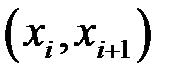 існує точка
існує точка 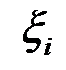 така, що
така, що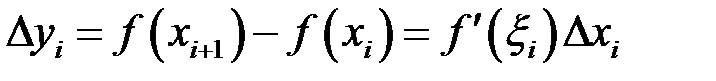 .
.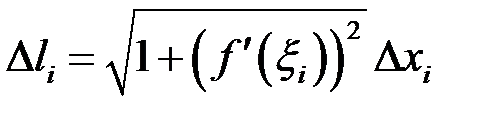 ,
,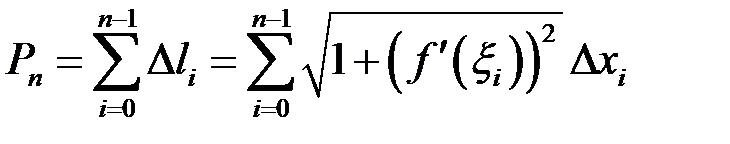 .
.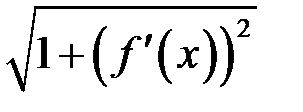 . Оскільки
. Оскільки 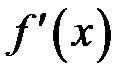 неперервна, функція
неперервна, функція 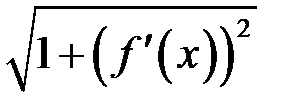 також неперервна, і тоді існує границя (15.1):
також неперервна, і тоді існує границя (15.1):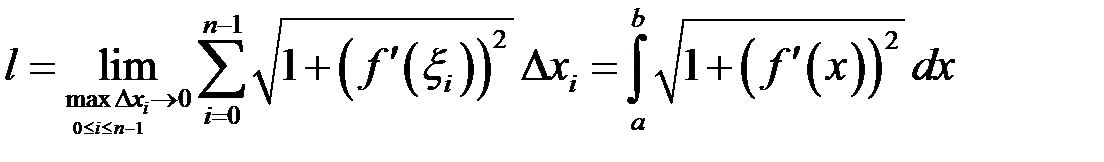 .
.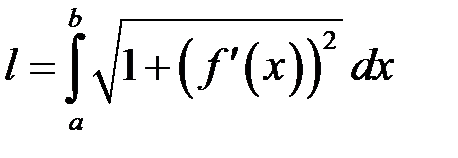 . (15.2)
. (15.2)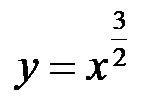 на відрізку
на відрізку 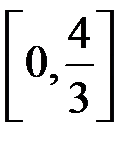 (рис. 16).
(рис. 16).
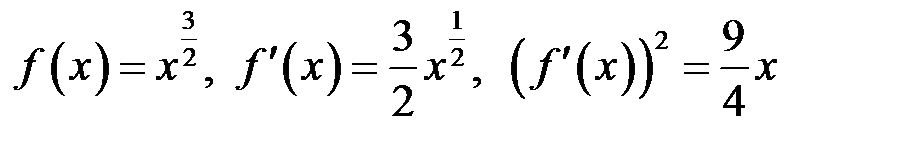 . Отже
. Отже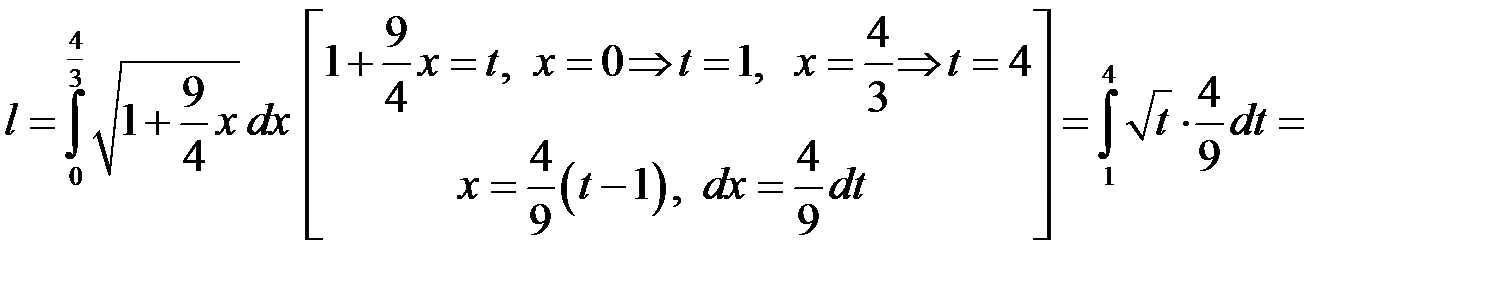
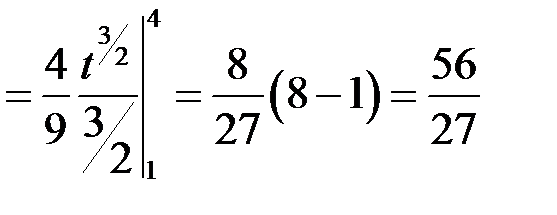 .
.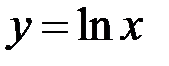 на відрізку
на відрізку 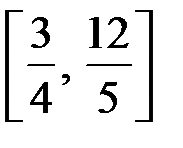 .
.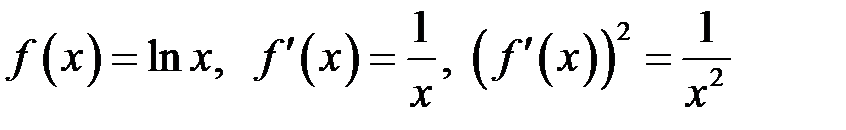 . Отже
. Отже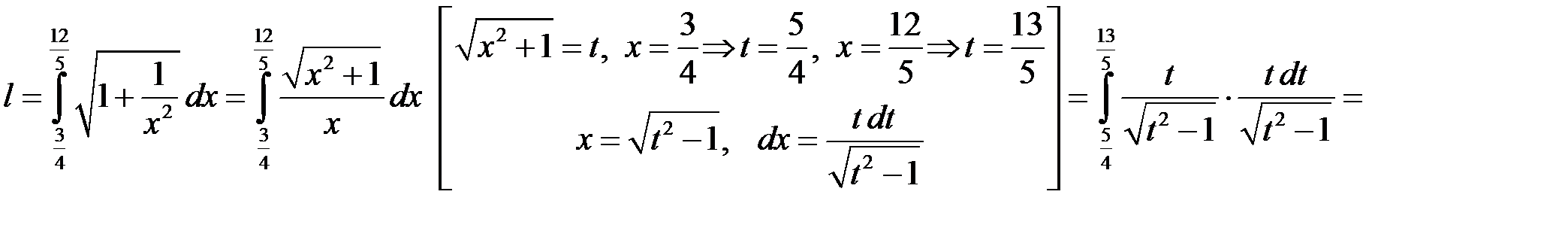
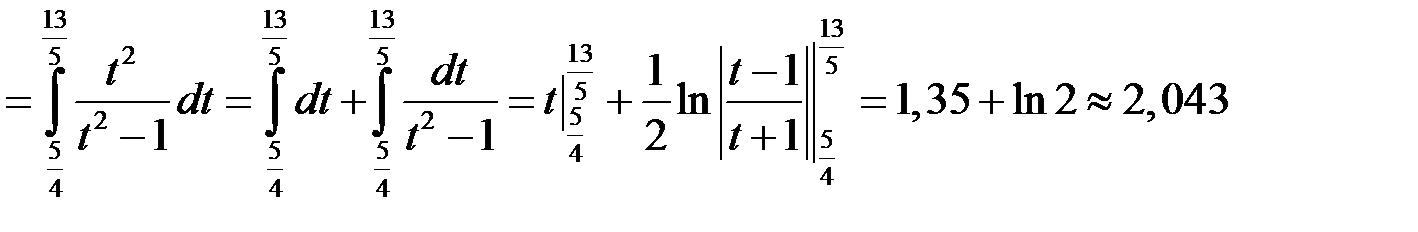 .
.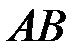 задано параметрично:
задано параметрично: 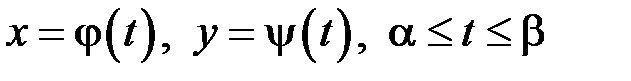 , де
, де 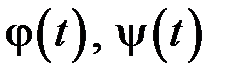 – неперервно диференційовні на проміжку
– неперервно диференційовні на проміжку 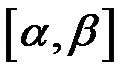 функції, то:
функції, то: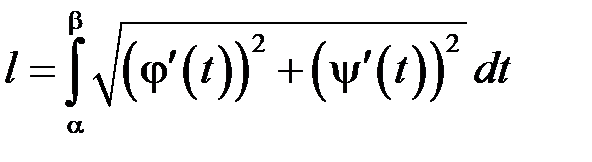 . (15.3)
. (15.3)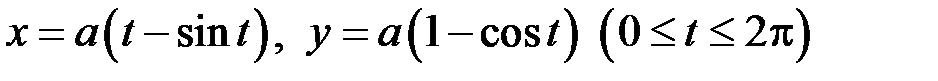 .
.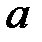 , яке котиться вздовж прямої лінії. У якості параметра
, яке котиться вздовж прямої лінії. У якості параметра 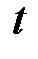 виступає кут поворота кола (рис. 17).
виступає кут поворота кола (рис. 17).
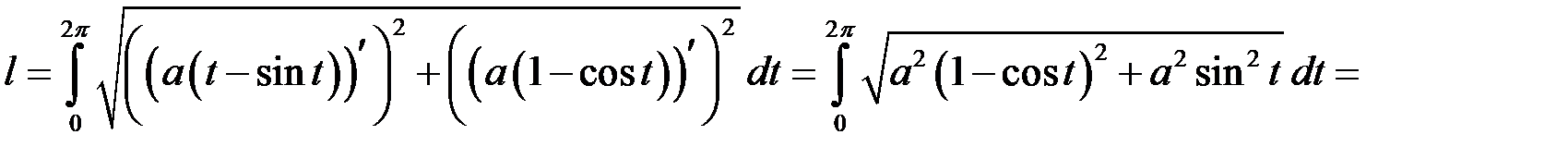
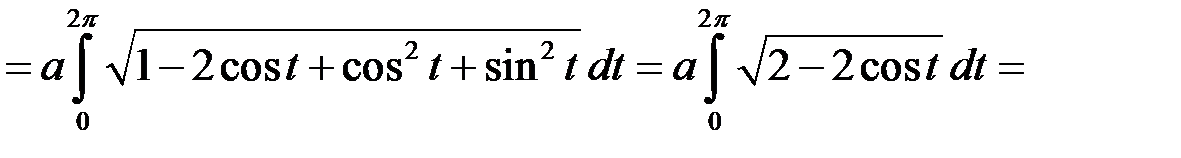
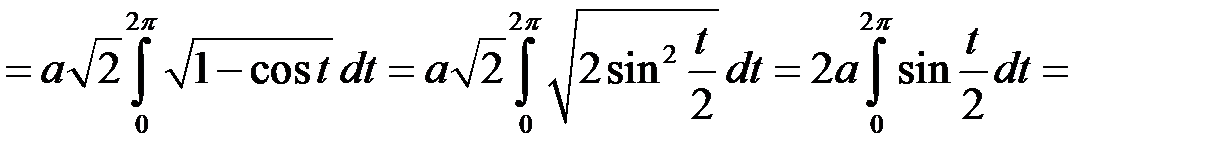
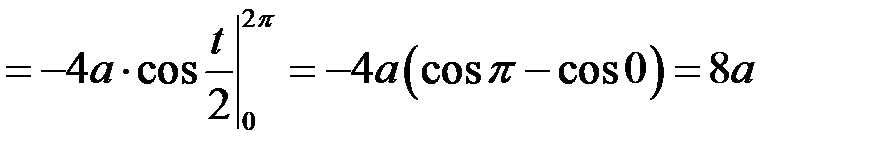 .
.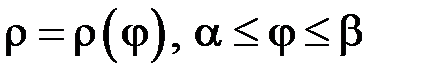 , де
, де 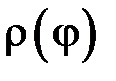 – неперервно диференційовна на
– неперервно диференційовна на 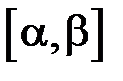 функція, то можна довести, що
функція, то можна довести, що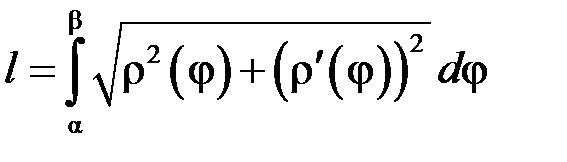 . (15.4)
. (15.4)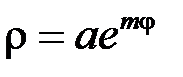
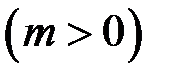 за умовою
за умовою 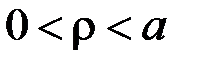 (рис. 18).
(рис. 18).
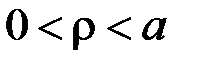 , дістаємо:
, дістаємо: 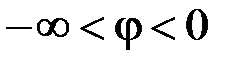 , отже за формулою (15.4) матимемо:
, отже за формулою (15.4) матимемо: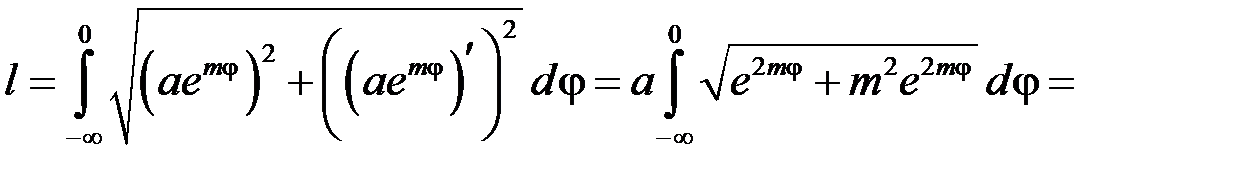
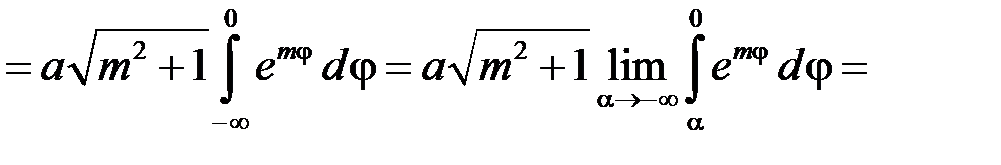
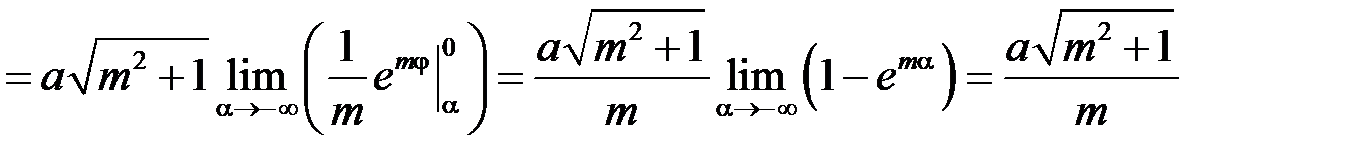
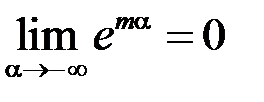 . Зауважимо, що інтеграл, який тут виникає – невласний 1-го роду.
. Зауважимо, що інтеграл, який тут виникає – невласний 1-го роду.