Тут ми сформулюємо деякі важливі властивості визначеного інтеграла, які нам будуть потрібні у подальшому.
1. Величина визначеного інтеграла не залежить від позначення змінної інтегрування.
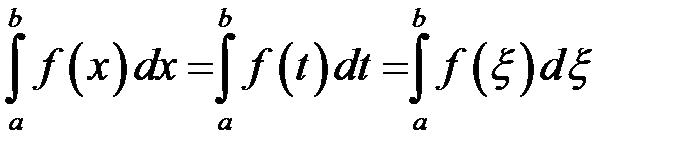 .
.
2. Якщо верхня межа інтегрування співпадає з нижньою, то інтеграл дорівнює нулю.
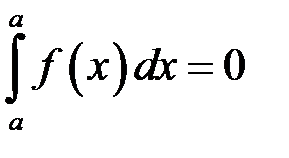 .
.
3. Від переставлення місцями меж інтегрування отримується інтеграл, який дорівнює даному з протилежним знаком.
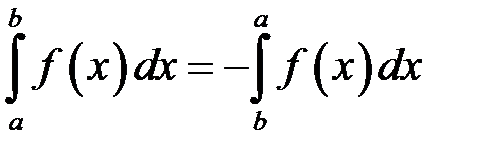 .
.
4. Якщо функція 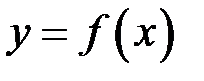 інтегровна на максимальному з відрізків
інтегровна на максимальному з відрізків 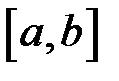 ,
, 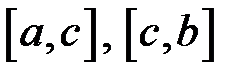 , то справедлива рівність:
, то справедлива рівність:
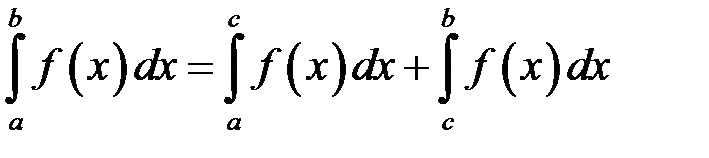 . (4.1)
. (4.1)
Доведення.Припустимо спочатку, що 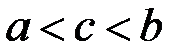 . Розіб’ємо відрізок
. Розіб’ємо відрізок 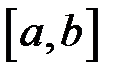 на частинні так, щоб точка
на частинні так, щоб точка 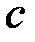 була точкою розбиття, наприклад
була точкою розбиття, наприклад 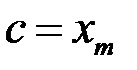 . Тоді
. Тоді
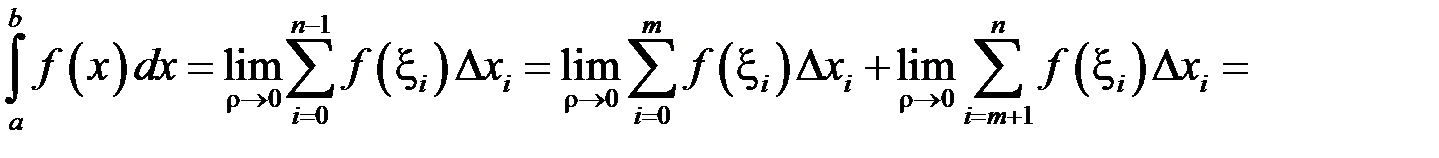
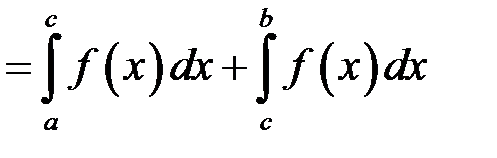 .
.
Цей факт добре ілюструється геометрично (рис. 4).
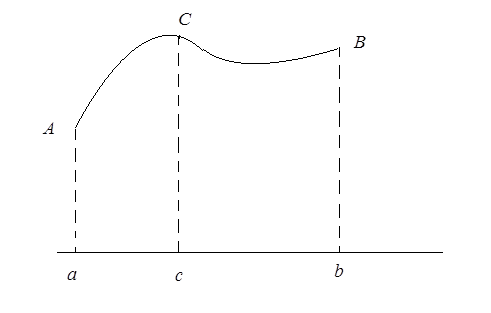
Рис. 4.
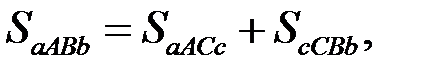
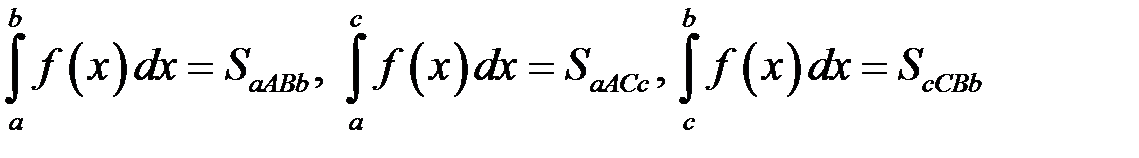 .
.
Формула (4.1) зберігає справедливість і у випадку, коли 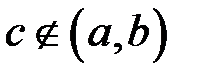 . Припустимо, наприклад що
. Припустимо, наприклад що 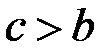 . Тоді згідно за попереднім:
. Тоді згідно за попереднім:
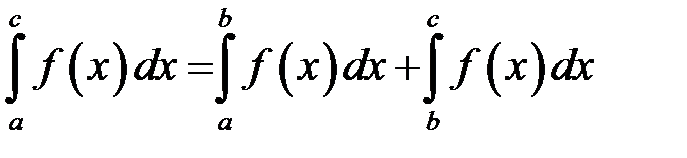 .
.
На підставі властивості 3 маємо:
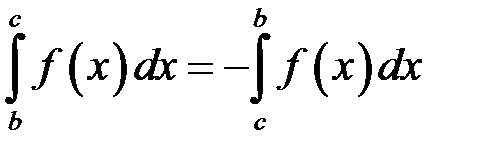 , і тоді:
, і тоді:
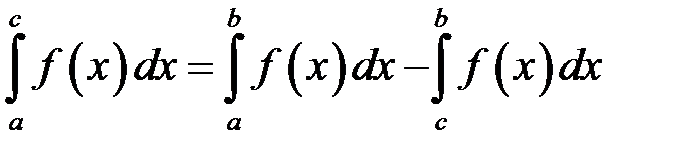 , а звідси і випливає формула (4.1). Випадок
, а звідси і випливає формула (4.1). Випадок  розглядається аналогічно.
розглядається аналогічно.
5. Сталий множник можна виносити за знак визначеного інтеграла:
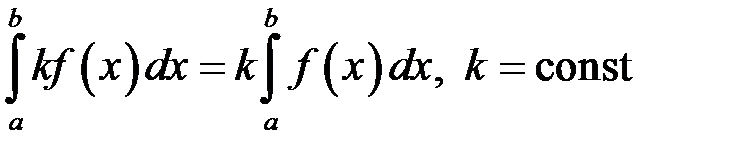 .
.
6. Якщо функції 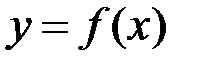 та
та 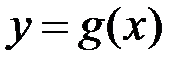 інтегровні на відрізку
інтегровні на відрізку 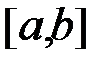 , то функції
, то функції 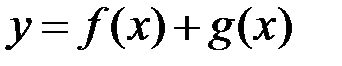 ,
, 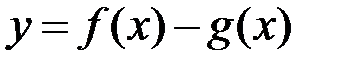 також інтегровні на відрізку
також інтегровні на відрізку 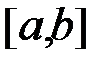 , причому:
, причому:
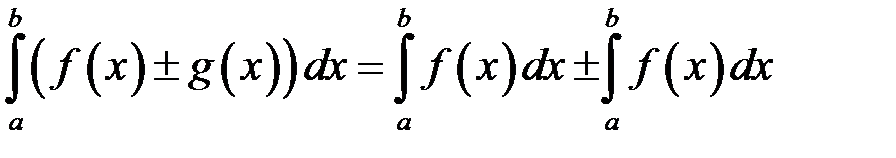 .
.
7. Якщо функції 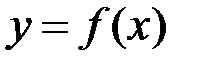 та
та 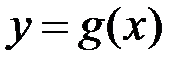 інтегровні на відрізку
інтегровні на відрізку 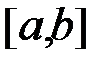 , то функція
, то функція 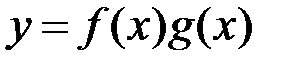 також інтегровна на відрізку
також інтегровна на відрізку 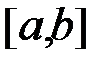 .
.
8. Якщо 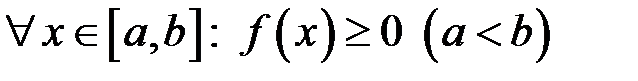 , то
, то
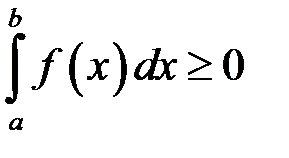 .
.
9. Якщо 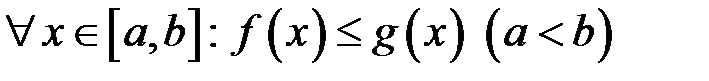 , то
, то
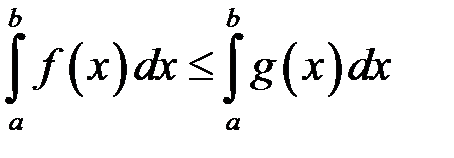 .
.
10. Якщо функція 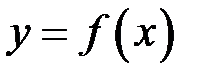 інтегровна на
інтегровна на 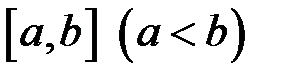 , то функція
, то функція 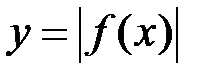 також інтегровна на відрізку
також інтегровна на відрізку 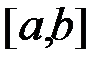 , причому:
, причому:
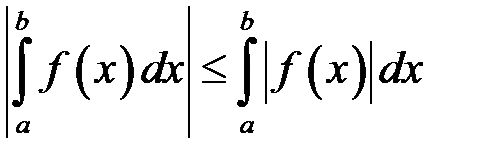 .
.
11. Якщо 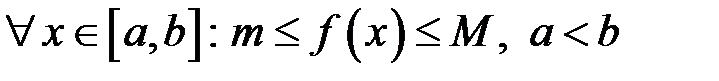 , то
, то
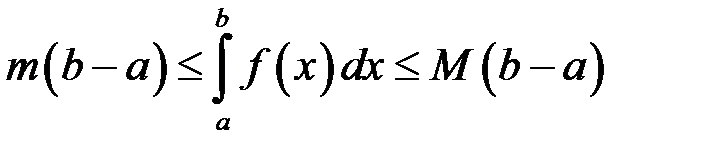 .
.
Дійсно
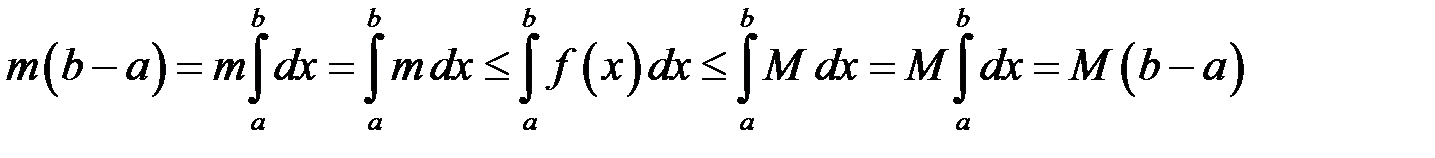 .
.
12. Теорема (про середнє значення функції). Нехай функція 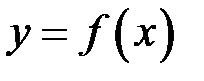 неперервна на відрізку
неперервна на відрізку 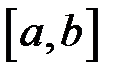 , а функція
, а функція 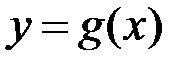 інтегровна на відрізку
інтегровна на відрізку 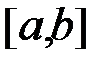 , і на відрізку
, і на відрізку 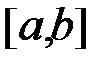 зберігає свій знак, тобто
зберігає свій знак, тобто 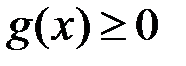 при
при 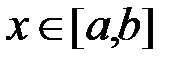 , або
, або 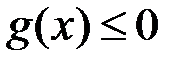 при
при 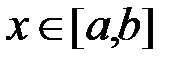 . Тоді на відрізку
. Тоді на відрізку 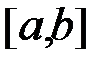 існує точка
існує точка 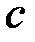 така, що виконуватиметься рівність:
така, що виконуватиметься рівність:
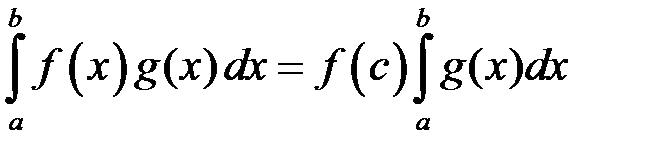 .
.
Доведення. Нехай для визначеності 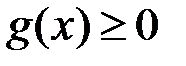 при
при 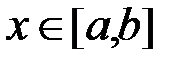 . Оскільки функція
. Оскільки функція 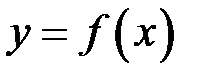 неперервна на відрізку
неперервна на відрізку 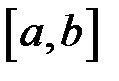 , то згідно з 2-ю теоремою Вейєрштрасса ця функція досягає на цьому відрізку свого найменшого та найбільшого значень
, то згідно з 2-ю теоремою Вейєрштрасса ця функція досягає на цьому відрізку свого найменшого та найбільшого значень 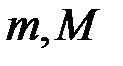 . Тоді:
. Тоді:
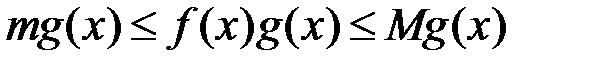 .
.
Внаслідок неперервності функції 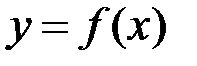 на відрізку
на відрізку 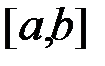 вона на цьому відрізку інтегровна, а, оскільки функція
вона на цьому відрізку інтегровна, а, оскільки функція 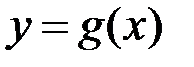 на відрізку
на відрізку 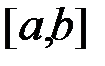 також інтегровна, то інтегровною на
також інтегровна, то інтегровною на 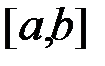 буде й функція
буде й функція 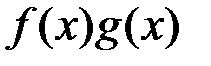 . А тоді
. А тоді
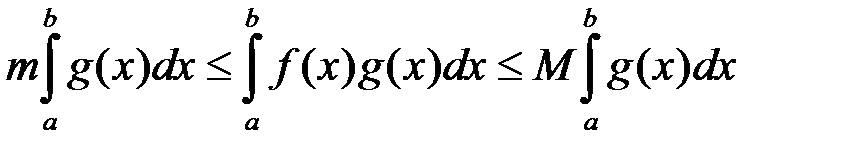 . (4.2)
. (4.2)
Якщо 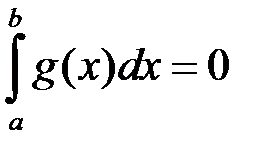 , то з (4.2) випливає, що
, то з (4.2) випливає, що 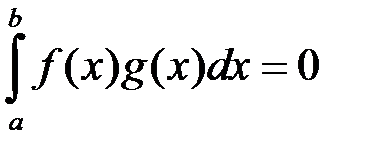 , і тоді твердження теореми доведено. Нехай
, і тоді твердження теореми доведено. Нехай 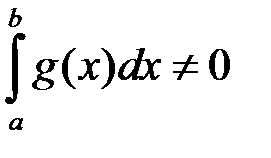 , тоді
, тоді 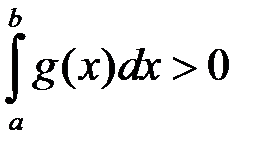 , оскільки
, оскільки 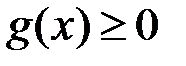 . Тому:
. Тому:
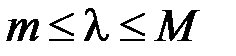 ,
,
де
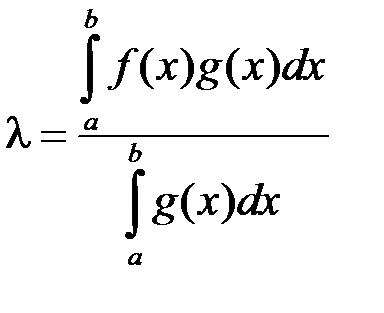 .
.
Внаслідок неперервності функції 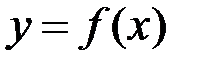 на відрізку
на відрізку 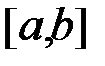 на підставі 2-ї теореми Больцано–Коші на відрізку
на підставі 2-ї теореми Больцано–Коші на відрізку 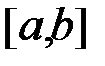 існує точка
існує точка 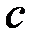 така, що
така, що 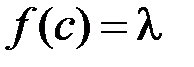 , тобто
, тобто
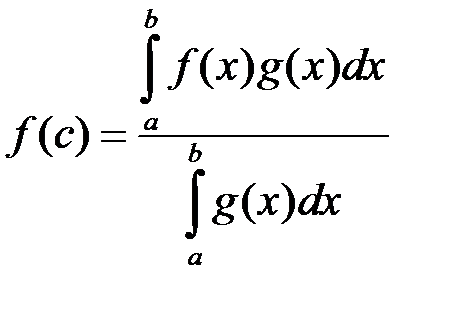 ,
,
звідки й випливає твердження теореми.
Наслідок. Якщо, зокрема 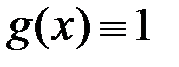 на
на 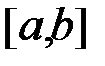 , то для неперервної на
, то для неперервної на 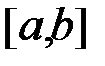 функції
функції 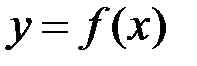 існує
існує 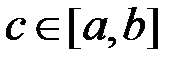 таке, що:
таке, що:
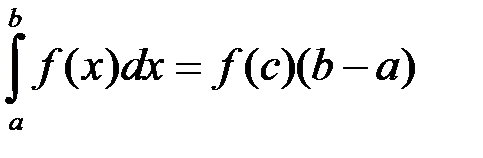 ,
,
оскільки 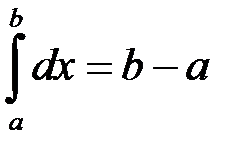 (див. п.3).
(див. п.3).
Величина 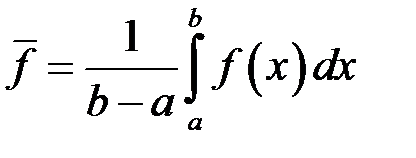 називається середнім значенням функції
називається середнім значенням функції 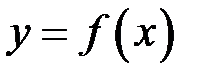 на відрізку
на відрізку 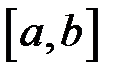 .
.
Теорема про середнє значення та наслідок з неї дає можливість оцінювати величини інтегралів без їх безпосереднього обчислювання.
Приклад. Оцінити величину інтеграла:
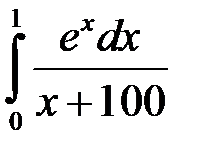 .
.
Покладемо в теоремі про середнє значення 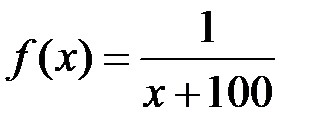 ,
, 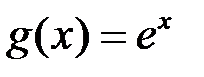 . Тоді
. Тоді 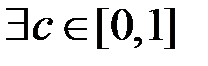 :
:
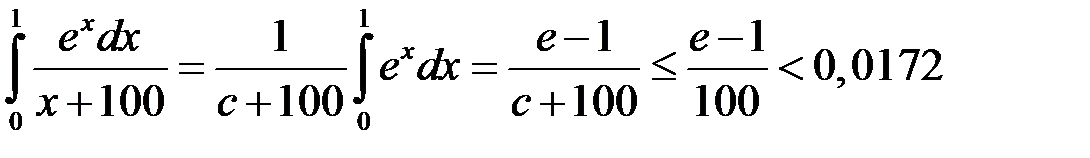
(тут скористалися рівністю 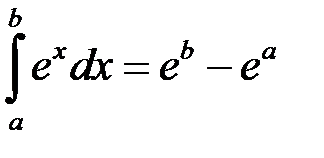 – див. п.3).
– див. п.3).


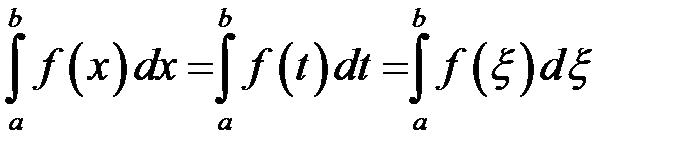 .
.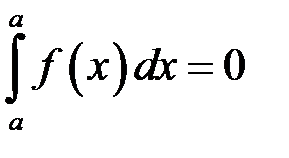 .
.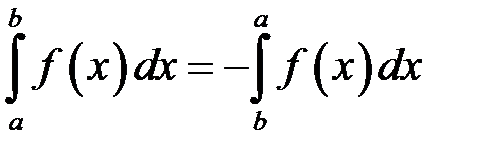 .
.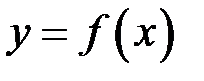 інтегровна на максимальному з відрізків
інтегровна на максимальному з відрізків 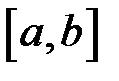 ,
, 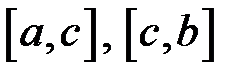 , то справедлива рівність:
, то справедлива рівність: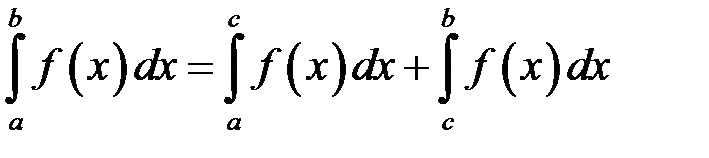 . (4.1)
. (4.1)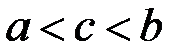 . Розіб’ємо відрізок
. Розіб’ємо відрізок 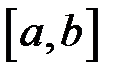 на частинні так, щоб точка
на частинні так, щоб точка 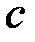 була точкою розбиття, наприклад
була точкою розбиття, наприклад 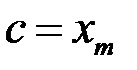 . Тоді
. Тоді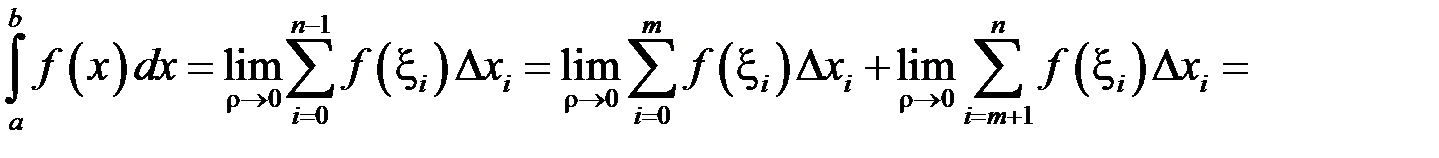
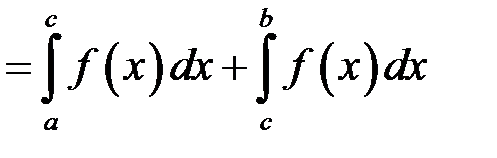 .
.
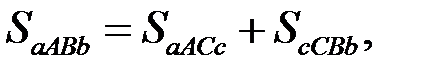
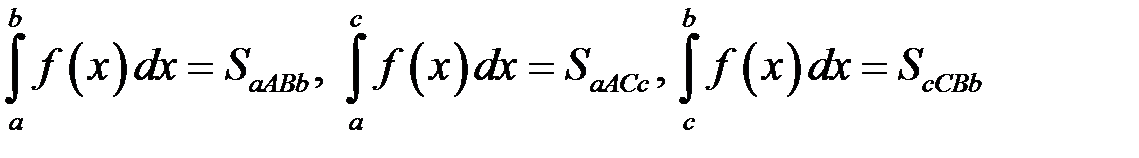 .
.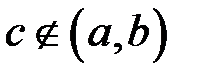 . Припустимо, наприклад що
. Припустимо, наприклад що 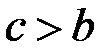 . Тоді згідно за попереднім:
. Тоді згідно за попереднім: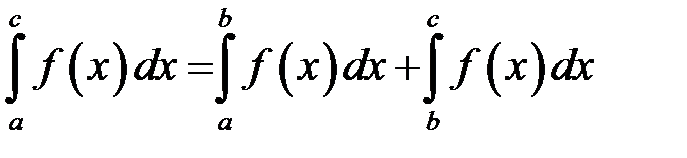 .
.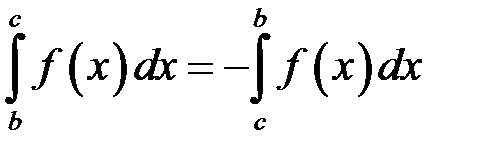 , і тоді:
, і тоді: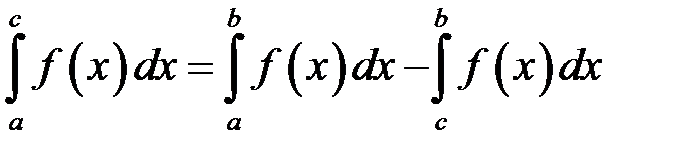 , а звідси і випливає формула (4.1). Випадок
, а звідси і випливає формула (4.1). Випадок  розглядається аналогічно.
розглядається аналогічно.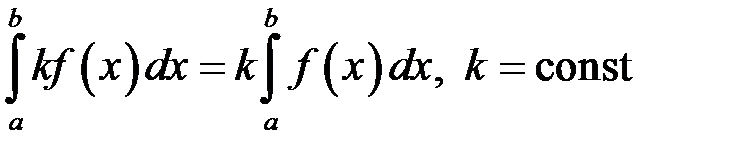 .
.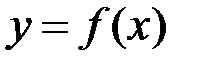 та
та 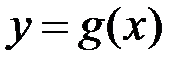 інтегровні на відрізку
інтегровні на відрізку 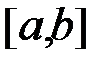 , то функції
, то функції 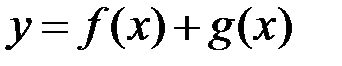 ,
, 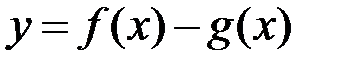 також інтегровні на відрізку
також інтегровні на відрізку 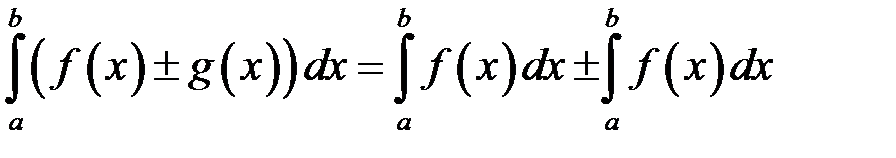 .
.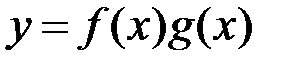 також інтегровна на відрізку
також інтегровна на відрізку 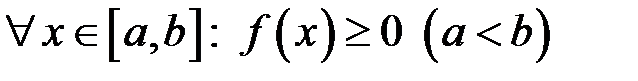 , то
, то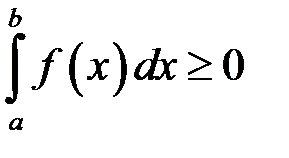 .
.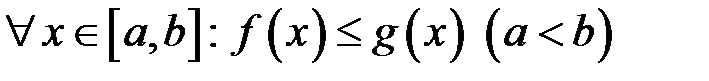 , то
, то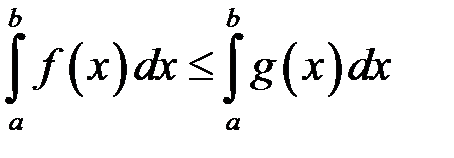 .
.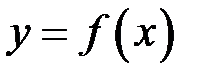 інтегровна на
інтегровна на 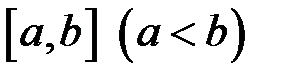 , то функція
, то функція 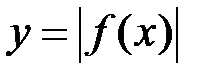 також інтегровна на відрізку
також інтегровна на відрізку 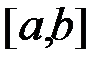 , причому:
, причому: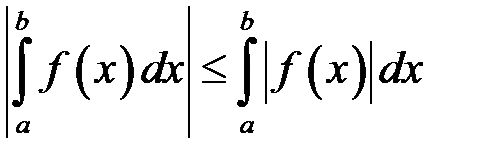 .
.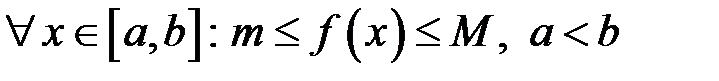 , то
, то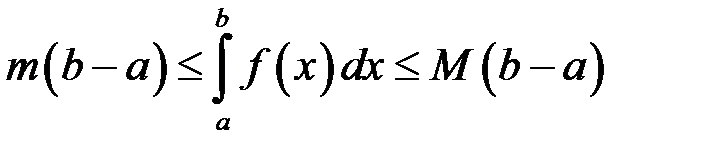 .
.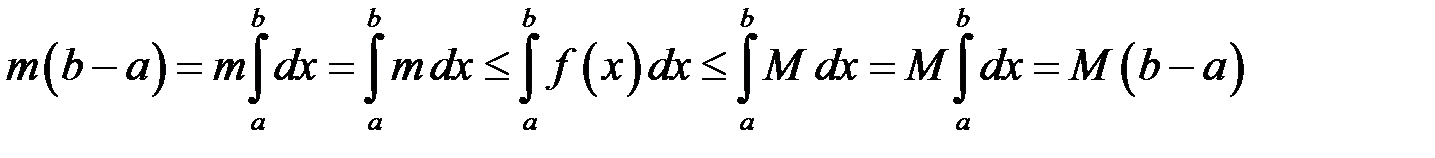 .
.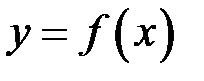 неперервна на відрізку
неперервна на відрізку 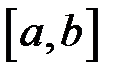 , а функція
, а функція 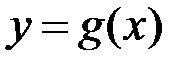 інтегровна на відрізку
інтегровна на відрізку 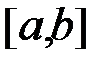 , і на відрізку
, і на відрізку 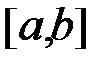 зберігає свій знак, тобто
зберігає свій знак, тобто 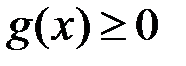 при
при 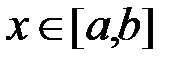 , або
, або 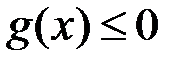 при
при 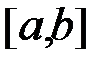 існує точка
існує точка 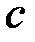 така, що виконуватиметься рівність:
така, що виконуватиметься рівність: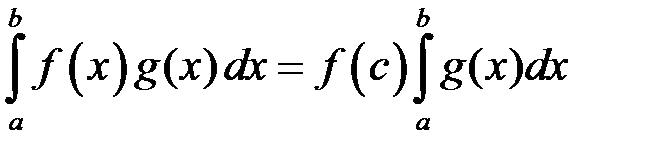 .
.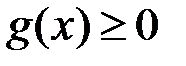 при
при 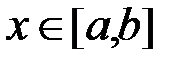 . Оскільки функція
. Оскільки функція 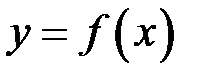 неперервна на відрізку
неперервна на відрізку 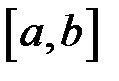 , то згідно з 2-ю теоремою Вейєрштрасса ця функція досягає на цьому відрізку свого найменшого та найбільшого значень
, то згідно з 2-ю теоремою Вейєрштрасса ця функція досягає на цьому відрізку свого найменшого та найбільшого значень 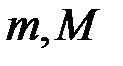 . Тоді:
. Тоді: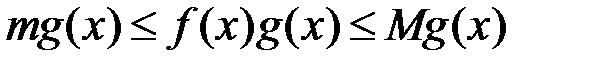 .
.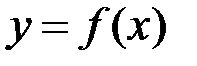 на відрізку
на відрізку 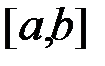 вона на цьому відрізку інтегровна, а, оскільки функція
вона на цьому відрізку інтегровна, а, оскільки функція 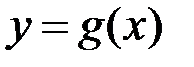 на відрізку
на відрізку 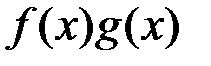 . А тоді
. А тоді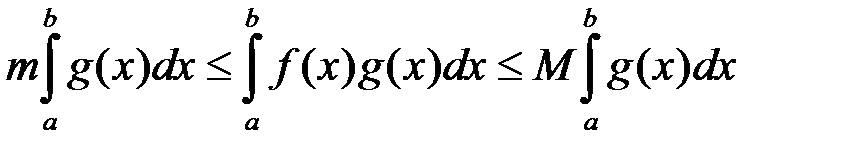 . (4.2)
. (4.2)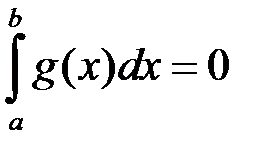 , то з (4.2) випливає, що
, то з (4.2) випливає, що 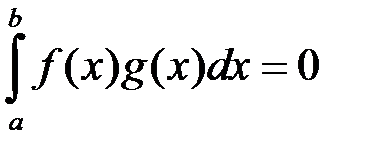 , і тоді твердження теореми доведено. Нехай
, і тоді твердження теореми доведено. Нехай 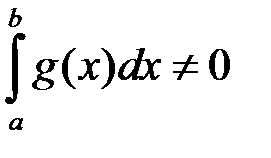 , тоді
, тоді 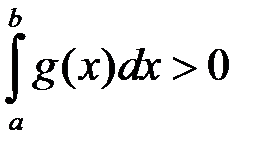 , оскільки
, оскільки 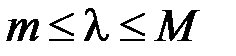 ,
,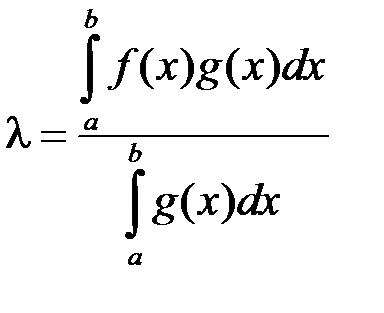 .
.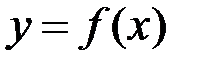 на відрізку
на відрізку 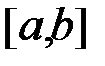 на підставі 2-ї теореми Больцано–Коші на відрізку
на підставі 2-ї теореми Больцано–Коші на відрізку 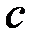 така, що
така, що 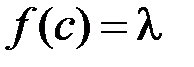 , тобто
, тобто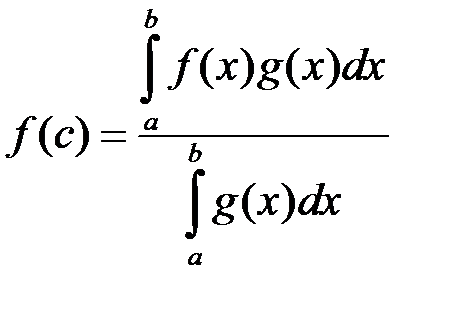 ,
,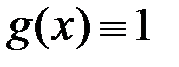 на
на 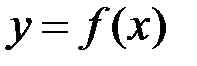 існує
існує 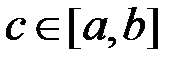 таке, що:
таке, що: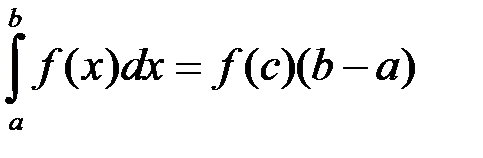 ,
,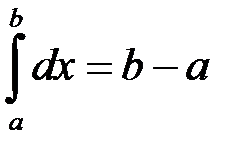 (див. п.3).
(див. п.3).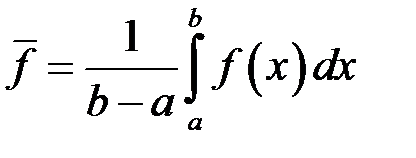 називається середнім значенням функції
називається середнім значенням функції 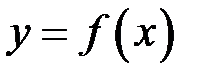 на відрізку
на відрізку 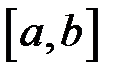 .
.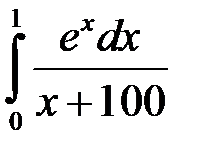 .
.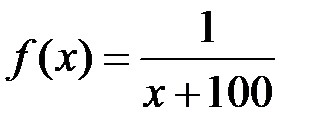 ,
, 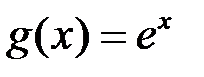 . Тоді
. Тоді 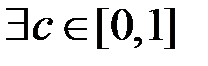 :
: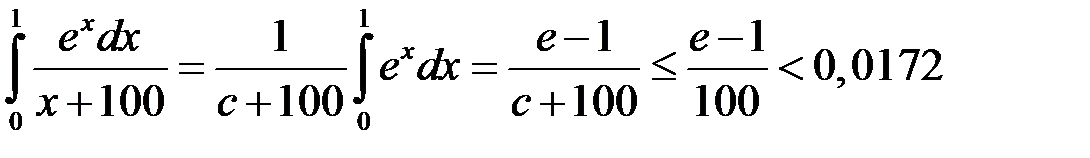
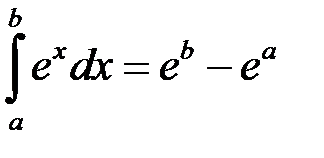 – див. п.3).
– див. п.3).