Наведемо приклади обчислення визначеного інтеграла, як кажуть, за означенням, тобто як границі інтегральних сум.
Приклад 1. Обчислити:
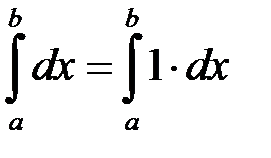 .
.
Розіб’ємо відрізок 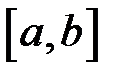 довільним чином на частинні відрізки і складемо інтегральну суму:
довільним чином на частинні відрізки і складемо інтегральну суму:
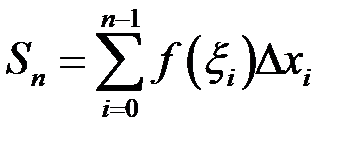 .
.
Незалежно від обрання точок 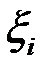 буде виконано:
буде виконано: 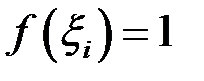 , тому:
, тому:
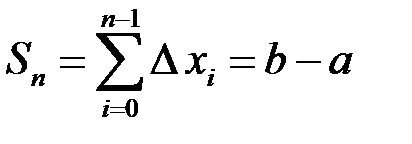 .
.
І отже:
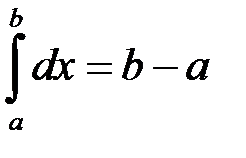 .
.
Приклад 2. Обчислити:
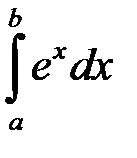 .
.
Оскільки функція 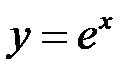 неперервна на всій числовій прямій, вона інтегровна на відрізку
неперервна на всій числовій прямій, вона інтегровна на відрізку 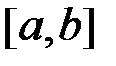 . Розіб’ємо відрізок
. Розіб’ємо відрізок 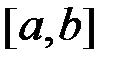 на
на 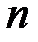 рівних частинних відрізків точками ділення
рівних частинних відрізків точками ділення 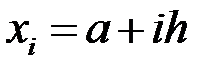
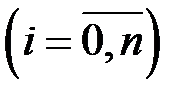 , де
, де 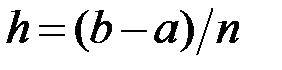 . Очевидно, що
. Очевидно, що 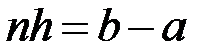 ,
, 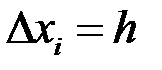
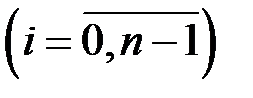 ,
, 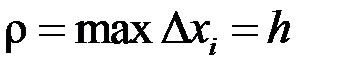 . За точки
. За точки 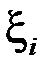 візьмемо
візьмемо 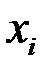
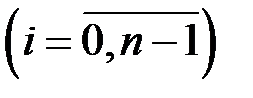 . Складемо інтегральну суму:
. Складемо інтегральну суму:
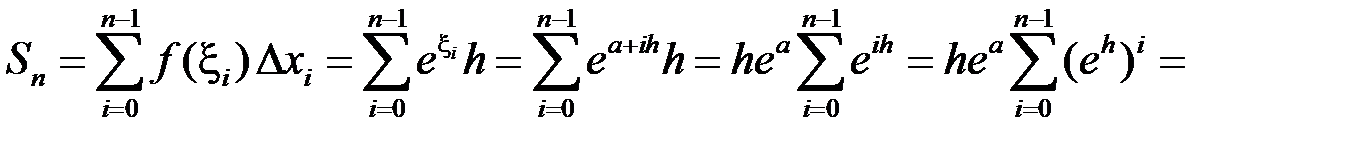
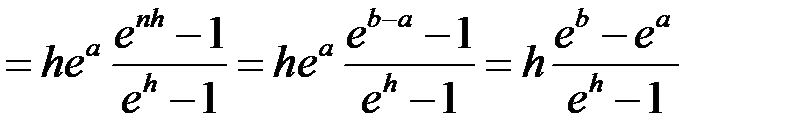 .
.
Тут ми скористалися формулою:
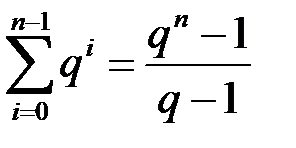 .
.
Тоді
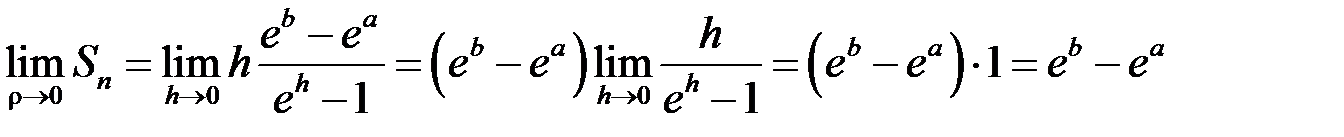 .
.
Отже
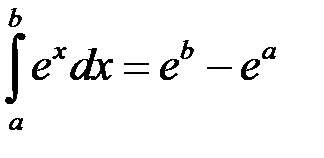 .
.
Приклад 3. Обчислити:
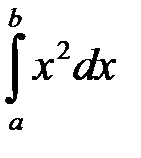 .
.
Оскільки функція 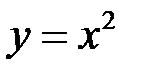 неперервна на всій числовій прямій, вона інтегровна на відрізку
неперервна на всій числовій прямій, вона інтегровна на відрізку 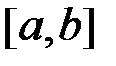 . Розіб’ємо відрізок
. Розіб’ємо відрізок 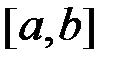 на
на 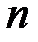 рівних частинних відрізків точками ділення
рівних частинних відрізків точками ділення 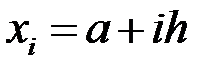
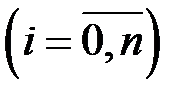 , де
, де 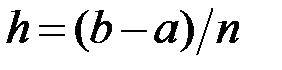 . Очевидно, що
. Очевидно, що 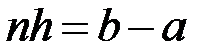 ,
, 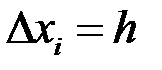
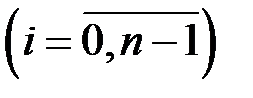 ,
, 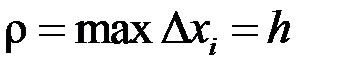 . Таким чином у даному випадку умова
. Таким чином у даному випадку умова 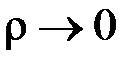 (або
(або 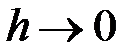 ) еквівалентна умові
) еквівалентна умові 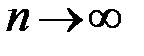 . За точки
. За точки 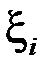 візьмемо
візьмемо 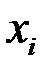
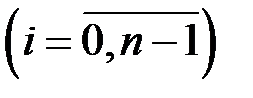 . Складемо інтегральну суму:
. Складемо інтегральну суму:
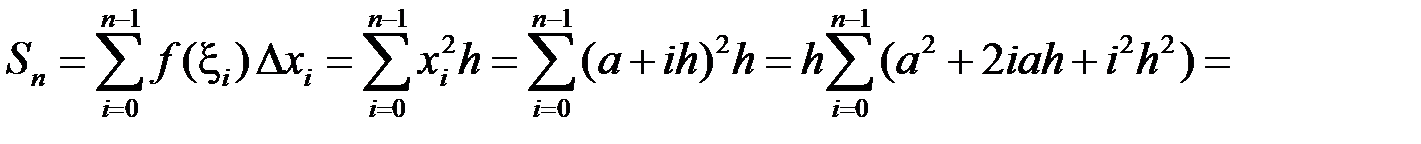
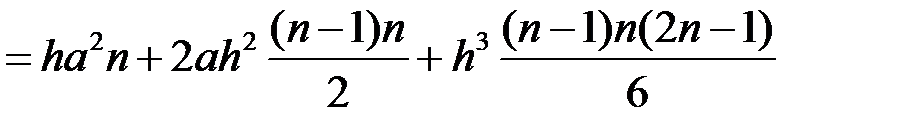 .
.
Тут скористалися формулами:
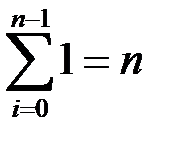 ,
, 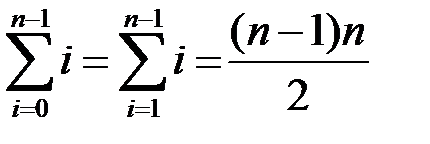 ,
, 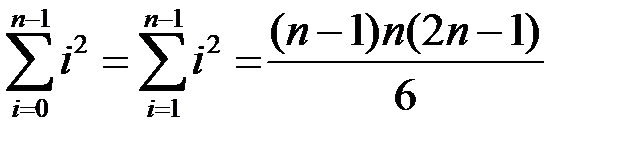 .
.
З урахуванням рівності 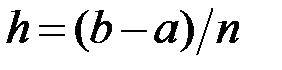 тепер маємо:
тепер маємо:
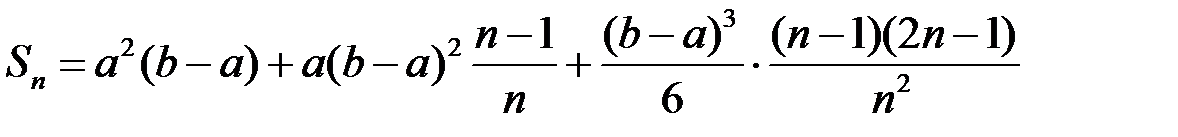 .
.
Звідси
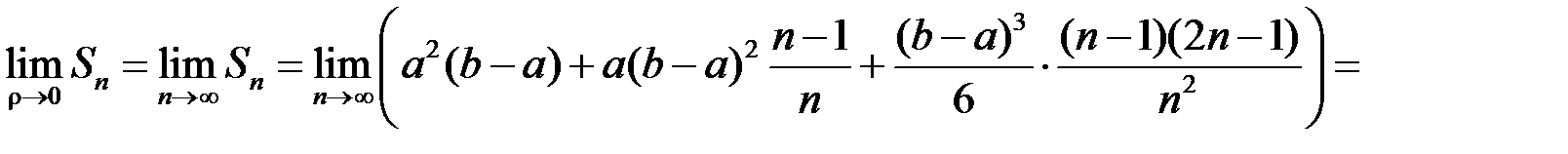
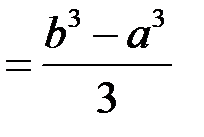 .
.
Отже
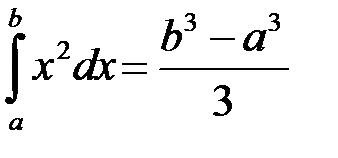 .
.
Вже ці приклади показують, що обчислення інтегралів за означенням досить складна задача, навіть для відносно простих функцій. Тому таким методом користуються рідко. Нижче ми наведемо формулу, за якою інтеграл обчислюється набагато простіше. Щоправда, ця формула виводиться у припущенні, що функція 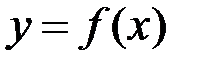 неперервна на відрізку
неперервна на відрізку 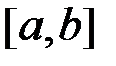 .
.


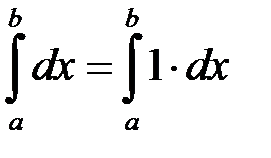 .
.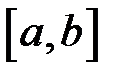 довільним чином на частинні відрізки і складемо інтегральну суму:
довільним чином на частинні відрізки і складемо інтегральну суму: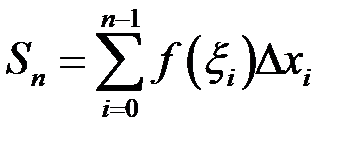 .
.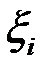 буде виконано:
буде виконано: 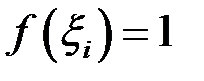 , тому:
, тому: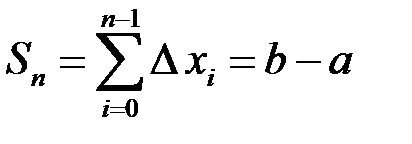 .
.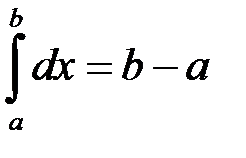 .
.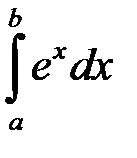 .
.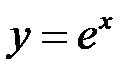 неперервна на всій числовій прямій, вона інтегровна на відрізку
неперервна на всій числовій прямій, вона інтегровна на відрізку 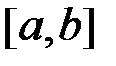 . Розіб’ємо відрізок
. Розіб’ємо відрізок 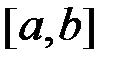 на
на 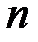 рівних частинних відрізків точками ділення
рівних частинних відрізків точками ділення 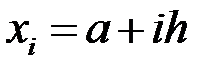
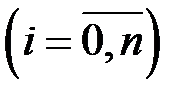 , де
, де 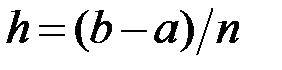 . Очевидно, що
. Очевидно, що 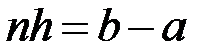 ,
, 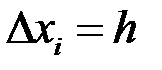
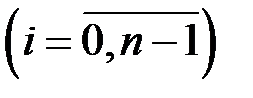 ,
, 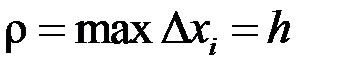 . За точки
. За точки 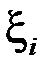 візьмемо
візьмемо 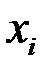
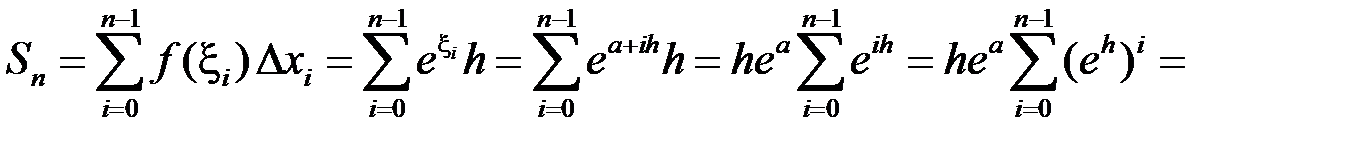
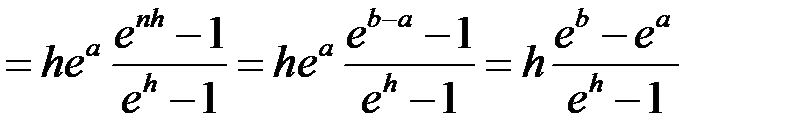 .
.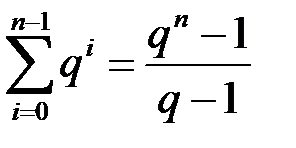 .
.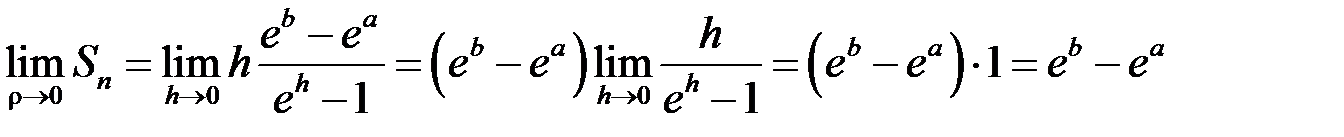 .
.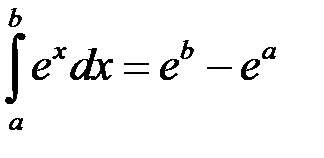 .
.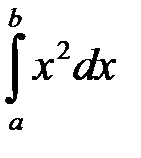 .
.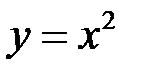 неперервна на всій числовій прямій, вона інтегровна на відрізку
неперервна на всій числовій прямій, вона інтегровна на відрізку 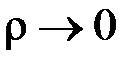 (або
(або 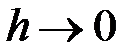 ) еквівалентна умові
) еквівалентна умові 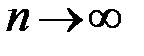 . За точки
. За точки 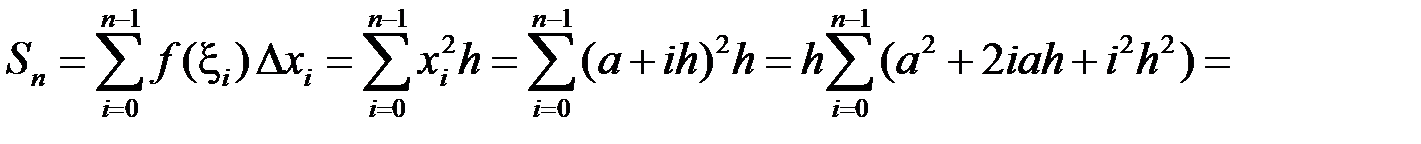
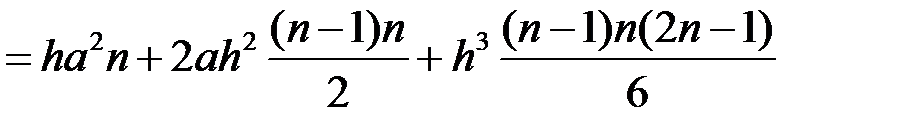 .
.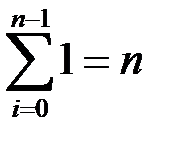 ,
, 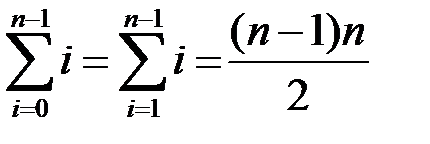 ,
, 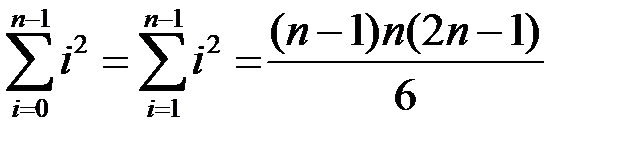 .
.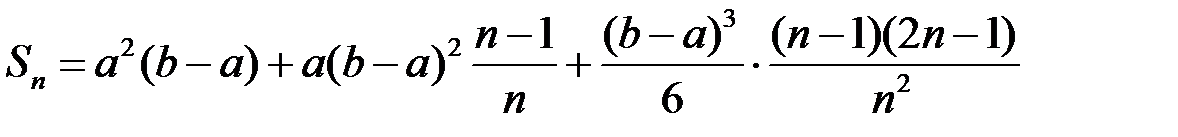 .
.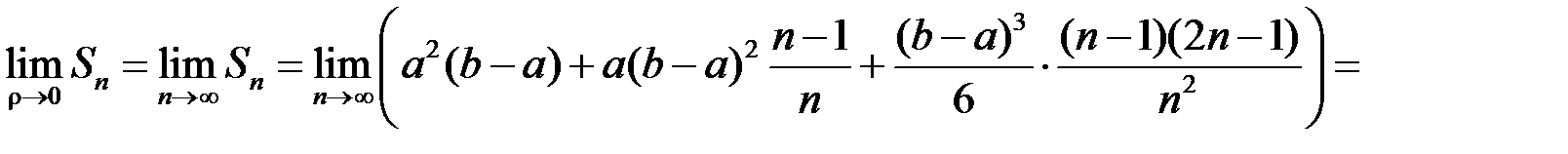
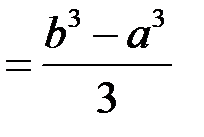 .
.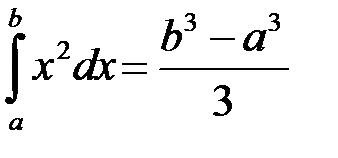 .
.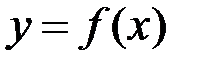 неперервна на відрізку
неперервна на відрізку 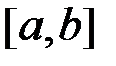 .
.