36. У правильній чотирикутній піраміді SABCD (S – вершина) бічне ребро вдвічі більше сторони основи. Знайдіть кут між медіаною трикутника SDC, проведеною з вершини D, та середньою лінією трикутника ASC, що паралельна основі піраміди.
Правильна відповідь : 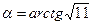 .
.
Розв’язання(авторський варіант)
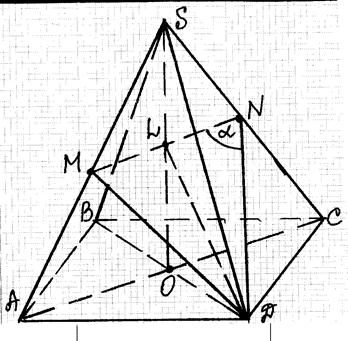
Нехай SABCD – задана правильна піраміда, в основі якої лежить квадрат ABCD, і SO її висота. Позначимо сторону основи АВ через а, тоді бічне ребро SA = 2a.
У трикутнику SDC з вершини D проведемо медіану DN, N – середина ребра SC. У трикутнику ASC проведемо середню лінію, паралельну AC. Вона перетинає ребра SA та SC у точках М та N відповідно, AM = MS та SN = NC (за означенням середньої лінії). Оскільки АС лежить у площині ABC і MN || AC, то MN || (ABC). Прямі MN та ND перетинаються в точці N, тому кут MND є шуканим кутом між медіаною DN трикутника SDC і середньою лінією MN трикутника ASC. Позначимо 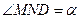 .
.
Діагональ АС квадрата АВСD дорівнює 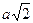 , тому середня лінія MN =
, тому середня лінія MN = 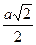 .
.
Висота SO піраміди перетинає MN в точці L. Оскільки трикутники ASC і SMN є рівнобедреними, то АО = ОС і ML = LN = 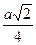 .
.
З прямокутного трикутника 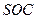
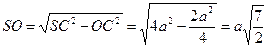 .
.
За теоремою Фалеса SL = LO = 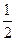 SO =
SO = 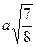 .
.
З прямокутного трикутника 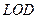
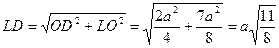 .
.
Трикутник DNM рівнобедрений, оскільки DM = DN як медіани рівних трикутників SAD та SCD. Медіана DL є висотою. Отже, трикутник DLN є прямокутним.
З трикутника DLN маємо:
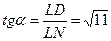 .
.
Відповідь. 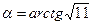 .
.


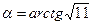 .
.
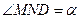 .
.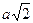 , тому середня лінія MN =
, тому середня лінія MN = 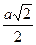 .
.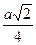 .
.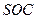
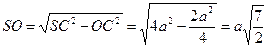 .
.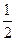 SO =
SO = 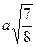 .
.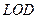
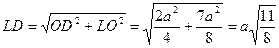 .
.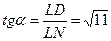 .
.