Є два види корму I і II, що містять живильні речовини (вітаміни) S1, S2, S3. Кількість одиниць живильних речовин в 1 кг кожного виду корму, необхідний мінімум живильних речовин наведені в табл. 6.2 (цифри умовні).
Таблиця 6.2 – Умовні дані задачі оптимізації складання раціону
| Живильна речовина (вітаміни)
| Необхідний мінімум живильних речовин
| Число одиниць живильних речовин в 1 кг корми
|
| I
| II
|
| S1
|
|
|
|
| S2
|
|
|
|
| S3
|
|
|
|
Вартість 1 кг корму I і II відповідно дорівнює 4 і 6 грн.
Необхідно скласти денний раціон, що має мінімальну вартість, у якому зміст кожного виду живильних речовин було б не менш установленої межі.
Складемо оптимізаційну модель задачі.
Позначимо:
x1, x2 – кількість кормів I і II, що входять у денний раціон.
Тоді цей раціон буде включати (3* x1+1* x2) одиниць живильної речовини S1, (1* x1+2* x2) одиниць речовин S2, (1* x1+6* x2) одиниць живильної речовини S3. У наслідок того, що кількість живильних речовин S1, S2, S3 у раціоні мусить бути не менш, відповідно 9, 8 і 12 одиниць, то маємо систему обмежень:
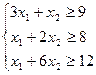 , (1)
, (1)
Змінні позитивні x1³0, x2³0.
Загальна вартість раціону F складе:
 . (2)
. (2)
Позначимо:
xj (j=1,2,…,n) – число одиниць корму n-го виду;
bi (i=1,2,…,m) – необхідний мінімум змісту в раціоні живильної речовини Si;
aij – число одиниць живильної речовини Sij в одиниці корму j-го виду;
cj- вартість одиниці корму j-го виду.
Математична модель задачі складання раціону в загальній постановці прийме наступний вид.
Знайти такий раціон X=(x1, x2,…,xj,…,xn),задовольняючій системі:
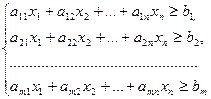
і умові
 ,
,
при якому функція
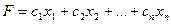
приймає мінімальне значення.
Задача оптимізації використання потужностей(задача про завантаження устаткування, складання розкладу).
Підприємству заданий план виробництва продукції за часом і номенклатурою: потрібно за час Т випустити n1, n2,…,nk одиниць продукції P1,P2,…,Pk. Продукція виробляється на верстатах S1,S2,…,Sm. Для кожного верстата відомі продуктивність aij і витрати bij на виготовлення продукції Pj на верстаті Si в одиницю часу.
Необхідно скласти такий план роботи верстатів (тобто так розподілити випуск продукції між верстатами), щоб витрати на виробництво всієї продукції були мінімальні.
Позначимо xij – час, протягом якого верстат Si – буде зайнятий виготовленням продукції Pj. У наслідок того, що час роботи кожного верстата обмежене й не перевищує Т, то справедливі обмеження:
 (3)
(3)
Для реалізації плану випуску по номенклатурі необхідно, щоб виконувалися наступні обмеження:
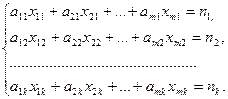 (4)
(4)
При цьому,
 (5)
(5)
Витрати на виробництво продукції виражаються функцією:
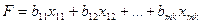 . (6)
. (6)


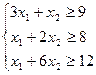 , (1)
, (1) . (2)
. (2)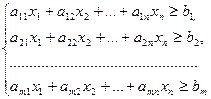
 ,
,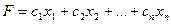
 (3)
(3)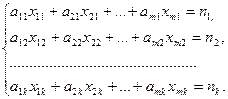 (4)
(4) (5)
(5)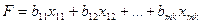 . (6)
. (6)