русс | укр
Программування
Мови програмуванняВідео уроки php mysqlПаскальСіАсемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование
Навчання
Linux
Unix
Алгоритмічні мови
Архітектура мікроконтролерів
Введення в розробку розподілених інформаційних систем
Дискретна математика
Інформаційне обслуговування користувачів
Інформація та моделювання в управлінні виробництвом
Комп'ютерна графіка
Лекції
|
Тема 4. Метод штучного базису. Параметричні задачі
Дата додавання: 2014-11-28; переглядів: 1553.
Питання 53
|
| Метод штучного базису. Штучні змінні вводяться до:
| |
| - усіх без винятку обмежень;
| |
| - усіх без винятку обмежень та до функції мети;
| |
| - до функції мети;
| |
| - до обмежень, що не містять базисних змінних, та до функції мети.
|
Питання 54
|
| Метод штучного базису. Функція мети прагне до max. Штучні змінні вводяться у функцію мети:
| |
| - зі знаком „+”;
| |
| - зі знаком „-”;
| |
| - байдуже з яким знаком;
| |
| - взагалі не вводяться.
|
Питання 55
|
| Метод штучного базису. Функція мети прагне до min. Штучні змінні вводяться у функцію мети:
| |
| - зі знаком „+”;
| |
| - зі знаком „-”;
| |
| - байдуже з яким знаком;
| |
| - взагалі не вводяться.
|
Питання 56
|
| Метод штучного базису. Для забезпечення виведення штучних змінних з базису використовують спосіб:
| |
| - введення штучних змінних до функції мети з дуже малим за модулем коефіцієнтом;
| |
| - введення штучних змінних до функції мети з дуже великим за модулем коефіцієнтом;
| |
| - введення штучних змінних до обмежень з дуже великим за модулем коефіцієнтом;
| |
| - введення штучних змінних до обмежень з дуже малим за модулем коефіцієнтом.
|
Питання 57
|
| Метод штучного базису дозволяє::
| |
| - об’єднати етап побудови базисного розв’язку та опорного плану і прискорює процедуру відшукання оптимального плану;
| |
| - лише об’єднати етап побудови базисного розв’язку та опорного плану;
| |
| - лише об’єднати етап побудови опорного та оптимального плану;
| |
| - відшукувати розв’язки лише задач, цільова функція яких прагне до max .
|
Питання 58
|
| Метод штучного базису. Після виведення штучної змінної з базису:
| |
| - вона, як правило, знову туди потрапляє через декілька ітерацій;
| |
| - вона лишається у функції мети;
| |
| - вона більше до базису не потрапляє (за винятком явища зациклення);
| |
| - вона виводиться лише з обмежень задачі..
|
Питання 59
|
| Принцип відшукання розв’язків задач з параметрами полягає у:
| |
| - поетапному відшуканні розв’язків задач на окремих проміжках значень параметрів;
| |
| - відшуканні розв’язків задач в окремих точках області допустимих значень планів задачі;
| |
| - відшуканні розв’язків у крайніх точках заданого інтервалу значень параметрів;
| |
| - у побудові окремих задач та відшукання їх розв’язків.
|
Питання 60
|
| Параметричними можуть бути::
| |
| - лише лінійні задачі;
| |
| - лише нелінійні задачі;
| |
| - лише транспортні задачі;
| |
| - будь-які задачі математичного програмування.
|
Питання 61
|
| Параметри у параметричних задачах можуть бути присутні:
| |
| - лише у обмеженнях;
| |
| - лише у виразі функції мети;
| |
| - лише у обсягах обмежень;
| |
| - як у виразі функції мети, так і у обмеженнях.
|
Тема 5. Двоїсть у лінійному програмуванні
Питання 62
|
| Продовжте! Двоїсть задач лінійного програмування:
| |
| - не взаємна;
| |
| - взаємна;
| |
| - довільна;
| |
| - не існує.
|
Питання 63
|
| План оптимальний, якщо він задовольняє:
| |
| - умови невиродженості плану;
| |
| - умови доповнюючої не жорсткості;
| |
| - умови лінійності;
| |
| - умови невід’ємності.
|
Питання 64
|
| Якщо пряма задача лінійного програмування має функцію мети, що прагне до max, і обмеження-нерівності типу „ 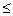 ” при невід’ємних змінних, то двоїста має: ” при невід’ємних змінних, то двоїста має:
| |
| - функцію мети на max і обмеження-нерівності типу „ 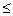 ” при невід’ємних змінних,; ” при невід’ємних змінних,;
| |
| - функцію мети на min і обмеження-нерівності типу „ 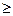 ”при невід’ємних змінних,; ”при невід’ємних змінних,;
| |
| - обмеження-рівняння при невід’ємних змінних;
| |
| - обмеження-рівняння і при недодатних змінних;
|
Питання 65
|
| Якщо пряма задача лінійного програмування має функцію мети, що прагне до min, і обмеження-нерівності типу „ 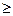 ” при невід’ємних змінних, то двоїста має: ” при невід’ємних змінних, то двоїста має:
| |
| - функцію мети на max і обмеження-нерівності типу „ 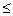 ” при невід’ємних змінних,; ” при невід’ємних змінних,;
| |
| - функцію мети на min і обмеження-нерівності типу „ 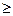 ”при невід’ємних змінних,; ”при невід’ємних змінних,;
| |
| - обмеження-рівняння при невід’ємних змінних;
| |
| - обмеження-рівняння і при недодатних змінних;
|
Питання 66
|
| Якщо пряма задача має несумісну систему умов, то двоїста до неї має:
| |
| - або необмежену систему умов або необмежену на множині своїх планів функцію мети;
| |
| - має несумісну систему умов;
| |
| - необмежену на множині свої планів функцію мети;
| |
| - має оптимальний план.
|
Питання 67
|
| Двоїсту та пряму задачі називають:
| |
| - парою сумісних задач;
| |
| - парою спряжених задач;
| |
| - парою протилежних задач;
| |
| - парою прикріплених задач.
|
Питання 68
|
| Якщо пряма задача має необмежену з боку оптимуму на множині своїх планів функцію мети, то двоїста до неї має:
| |
| - має несумісну систему умов;
| |
| - або необмежену систему умов або необмежену на множині своїх планів функцію мети;
| |
| - необмежену на множині свої планів функцію мети;
| |
| - має оптимальний план.
|
Питання 69
|
| Двоїсту задачу можна побудувати до:
| |
| - довільної задачі
| |
| - лише до задачі на max цільової функції;
| |
| - лише до задачі, записаної у 2-ій канонічній постаті;
| |
| - лише до стандартної задачі.
|
Питання 70
|
| Змінні двоїстої задачі по відношенню до обмежень-нерівностей типу „ 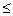 ” прямої задачі є: ” прямої задачі є:
| |
| - тіньовими оцінками коефіцієнтів функції мети;
| |
| - тіньовими цінами об’ємів шуканих величин;
| |
| - тіньовими оцінками ресурсів;
| |
| - не мають будь-якого економічного змісту.
|
Питання 71
|
| Остання симплексна таблиця. Коефіцієнти заміщення – це:
| |
| - коефіцієнти при небазисних змінних функції мети;
| |
| - коефіцієнти при небазисних змінних у обмеженнях;
| |
| - вільні члени;
| |
| - коефіцієнти при базисних змінних.
|
|
|
Онлайн сервіси
Онлайн система числення
Калькулятор онлайн звичайний
Науковий калькулятор онлайн
|


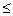 ” при невід’ємних змінних, то двоїста має:
” при невід’ємних змінних, то двоїста має:
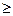 ”при невід’ємних змінних,;
”при невід’ємних змінних,;