русс | укр
Программування
Мови програмуванняВідео уроки php mysqlПаскальСіАсемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование
Навчання
Linux
Unix
Алгоритмічні мови
Архітектура мікроконтролерів
Введення в розробку розподілених інформаційних систем
Дискретна математика
Інформаційне обслуговування користувачів
Інформація та моделювання в управлінні виробництвом
Комп'ютерна графіка
Лекції
|
Тема 1. Предмет, метод математичного програмування. Класифікація задач математичного програмування. Постаті задач лінійного програмуванн.
Дата додавання: 2014-11-28; переглядів: 2392.
Таблица значений интеграла вероятностей Ф ( х ) = 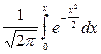
| х
| Ф ( х )
| х
| Ф ( х )
| х
| Ф ( х )
| | 0.00
| 0.0000
| 1.20
| 0.3849
| 2.40
| 0.4918
| | 0.05
| 0.0199
| 1.25
| 0.3944
| 2.45
| 0.4929
| | 0.10
| 0.0398
| 1.30
| 0.4032
| 2.50
| 0.4938
| | 0.15
| 0.0596
| 1.35
| 0.4115
| 2.55
| 0.4946
| | 0.20
| 0.0793
| 1.40
| 0.4192
| 2.60
| 0.4953
| | 0.25
| 0.0987
| 1.45
| 0.4265
| 2.65
| 0.4960
| | 0.30
| 0.1179
| 1.50
| 0.4332
| 2.70
| 0.4965
| | 0.35
| 0.1368
| 1.55
| 0.4394
| 2.75
| 0.4970
| | 0.40
| 0.1554
| 1.60
| 0.4452
| 2.80
| 0.4974
| | 0.45
| 0.1736
| 1.65
| 0.4505
| 2.85
| 0.4978
| | 0.50
| 0.1915
| 1.70
| 0.4554
| 2.90
| 0.4981
| | 0.55
| 0.2088
| 1.75
| 0.4599
| 2.95
| 0.4984
| | 0.60
| 0.2257
| 1.80
| 0.4641
| 3.00
| 0.4987
| | 0.65
| 0.2422
| 1.85
| 0.4678
| 3.05
| 0.4989
| | 0.70
| 0.2580
| 1.90
| 0.4713
| 3.10
| 0.4990
| | 0.75
| 0.2734
| 1.95
| 0.4744
| 3.15
| 0.4992
| | 0.80
| 0.2881
| 2.00
| 0.4773
| 3.20
| 0.4993
| | 0.85
| 0.3023
| 2.05
| 0.4798
| 3.25
| 0.4994
| | 0.90
| 0.3159
| 2.10
| 0.4821
| 3.30
| 0.4995
| | 0.95
| 0.3289
| 2.15
| 0.4842
| 3.35
| 0.4995
| | 1.00
| 0.3413
| 2.20
| 0.4861
| 3.40
| 0.4996
| | 1.05
| 0.3531
| 2.25
| 0.4878
| 3.45
| 0.4997
| | 1.10
| 0.3643
| 2.30
| 0.4893
| 3.50
| 0.4998
| | 1.15
| 0.3749
| 2.35
| 0.4906
| 3.75
| 0.4999
|
Библиографический список
1. Советов Б.Я., Яковлев С.А. Моделирование систем: учеб. для вузов – 3-е изд., перераб. и доп. – М.: Высш. шк., 2001.
2. Петров А.В. Моделирование систем: учеб. пособие. – Иркутск: Изд-во ИрГТУ. – 2000.
ПАКЕТ ТЕСТОВИХ ЗАВДАНЬ
з дисципліни „Математичне програмування”
для студентів спеціальності „Економічна кібернетика”
Тема 1. Предмет, метод математичного програмування. Класифікація задач математичного програмування. Постаті задач лінійного програмуванн.
Питання 1
|
| Роль математичного програмування полягає у:
| |
| - розробці методів розв’язання екстремальних задач;
| |
| - відшуканні області допустимих розв’язків задач;
| |
| - розробці методів розв’язання лінійних задач;
| |
| - побудові екстремальних задач.
|
Питання 2
|
| Задачі математичного програмування не класифікуються як:
| |
| - лінійні та нелінійні;
| |
| - кубічні та двоїчні;
| |
| - статичні та динамічні;
| |
| - стохастичні та детерміновані.
|
Питання 3
|
| Другу канонічну постать ЗЛП називають:
| |
| - двоїною;
| |
| - подвійною;
| |
| - симетричною;
| |
| - стандартною.
|
Питання 4
|
| Друга назва першої канонічної постаті ЗЛП:
| |
| - первинна;
| |
| - стандартна;
| |
| - стандартизована;
| |
| - узагальнена.
|
Питання 5
|
| Не вироджений план – це план, який містить кількість:
| |
| - ненульових компонент, що дорівнює рангу матриці задачі;
| |
| - нульових компонент, що більша рангу матриці задачі;
| |
| - невід’ємних компонент, що на одиницю більша рангу матриці задачі;
| |
| - від’ємних компонент, що на одиницю більша рангу матриці задачі;
|
Питання 6
|
| Стандартна постать ЗЛП включає вираз функції мети та:
| |
| - систему основних обмежень-рівнянь;
| |
| - систему основних обмежень-нерівностей обох типів, обмеження на невід’ємність змінних;
| |
| - систему основних обмежень-рівнянь, обмеження на невід’ємність змінних;
| |
| - систему основних обмежень-нерівностей обох типів, обмеження на недодатність змінних;
|
Питання 7
|
| Друга канонічна постать при прагненні цільової функції до max включає систему:
| |
| - основних обмежень-нерівностей типу 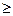 , обмеження на невід’ємність змінних; , обмеження на невід’ємність змінних;
| |
| - основних обмежень-нерівностей типу 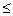 , обмеження на невід’ємність змінних; , обмеження на невід’ємність змінних;
| |
| - основних обмежень-рівнян, обмеження на невід’ємність змінних;
| |
| - будь-які обмеження.
|
Питання 8
|
| Друга канонічна постать при прагненні цільової функції до min включає систему:
| |
| - основних обмежень-нерівностей типу 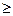 , обмеження на невід’ємність змінних; , обмеження на невід’ємність змінних;
| |
| - основних обмежень-нерівностей типу 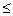 , обмеження на невід’ємність змінних; , обмеження на невід’ємність змінних;
| |
| - основних обмежень-рівнянь, обмеження на невід’ємність змінних;
| |
| - будь-які обмеження.
|
Питання 9
|
| При приведенні ЗЛП до стандартної постаті у обженні-нерівності типу 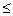 : :
| |
| - до лівої частини додається невід’ємна змінна;
| |
| - від лівої частини віднімається невід’ємна змінна;
| |
| - до лівої частини додається від’ємна змінна;
| |
| - від лівої частини віднімається невід’ємна змінна.
|
Питання 10
|
| При приведенні ЗЛП до стандартної постаті у обженні-нерівності типу 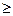 : :
| |
| - до лівої частини додається невід’ємна змінна;
| |
| - від лівої частини віднімається невід’ємна змінна;
| |
| - до лівої частини додається від’ємна змінна;
| |
| - від лівої частини віднімається невід’ємна змінна.
|
Питання 11
|
| При приведенні ЗЛП до стандартної постаті не додатна змінна:
| |
| - лишається у задачі незмінною;
| |
| - замінюється змінною, протилежною за знаком;
| |
| - замінюється оберненою змінною;
| |
| - замінюється добутком двох змінних.
|
Питання 12
|
| При приведенні ЗЛП до стандартної постаті змінна, необмежена за знаком може бути замінена:
| |
| - різницею двох невід’ємних змінних;
| |
| - добутком двох невід’ємних змінних;
| |
| - різницею двох недодатних змінних;
| |
| - добутком двох недодатних змінних.
|
Питання 13
|
| Загальна задача лінійного програмування включає функцію мети та:
| |
| - обмеження-нерівності обох типів при лише невід’ємних змінних;
| |
| - обмеження-нерівності обох типів при лише недодатних змінних;
| |
| - обмеження-нерівності обох типів та рівняння і змішану систему обмежень на знак змінних;
| |
| - обмеження-рівності при невід’ємних змінних.
|
|
|
Онлайн сервіси
Онлайн система числення
Калькулятор онлайн звичайний
Науковий калькулятор онлайн
|


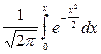
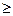 , обмеження на невід’ємність змінних;
, обмеження на невід’ємність змінних;
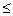 , обмеження на невід’ємність змінних;
, обмеження на невід’ємність змінних;