Структурний підхід при побудові алгоритмів - це підхід, який дозволяє "дисциплінувати" процес створення (побудови) алгоритму. Сам по собі структурний підхід не є обов' язковим при складанні алгоритмів, але його застосування значно полегшує як читання, так і аналіз алгоритму виконавцями.
Структурний підхід включає в себе ряд структурних елементів ,які базуються на раніше введених символах. До основних отруктурних елементів відносяться: слідування. Всі символи і блоки алгоритму повинні бути послідовно розміщеними, тобто алгоритм повинен читатись зліва-направо і зверху-вниз
розгалуження. Застосовується, коли в залежності від виконання умови (істинності умови) необхідно виконати одну або іншу дію. Кожна з цих дій, в свою чергу, може містити декілька етапів
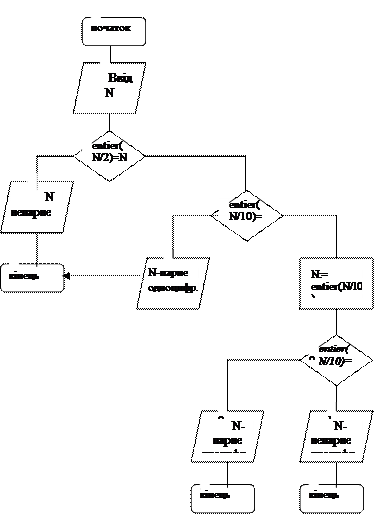
Блок-схема перевірки N на парність і двоцифровість.
обхід. Це частковий випадок розгалуження, коли одна з віток , як
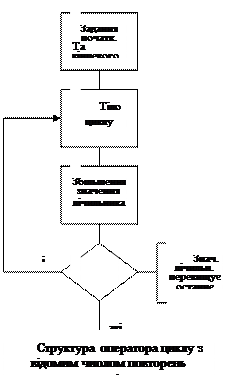
правило, містить жодних дій. Вказану конструкцію можна використовувати швидше,як виняток. цикли. Тіло циклу - це сукупність етапів, які необхідно багаторазово повторювати в процесі виконання алгоритму. Число повторень тіла циклу задаєтьcя умовою, яка називається умовою завершення циклу. Перед виконанням циклу ряду змінних, які в нього входять, необхідно присвоїти початкові значення. Цей етап називається етапом ініціалізації циклу.
Два типи циклів використовуються в алгоритмізаціі. Це цикли з відомим числом повторень (іноді їх ще називають циклами типу перерахунку або циклами типу До) і цикли з невідомим числом повторень (ітераційні цикли або цикли типу ПОКИ).
Цикли з відомим числом повторень
Використовуються в тих випадках, коли число повторень тіла циклу відоме. Цикли вказаного типу містять лічильник числа повторень тіла циклу, який може змінювати свої значення лише в строго заданому інтервалі. Тому перед виконанням групи операторів тіла циклу необхідно зарезервувати в алгоритмі ряд змінних, які будуть з6ерігати початкове і кінцеве значення керуючої змінної, а також величину кроку, при допомозі якого ми від початкового значення керуючої змінної приходимо до її кінцевого значення. Цей процес називається етапом ініціалізації. В ролі початкового, кінцевого значення керуючої змінної і кроку можна використовувати константи, але в ряді випадків застосування констант суттєво звужує область застосування алгоритму.
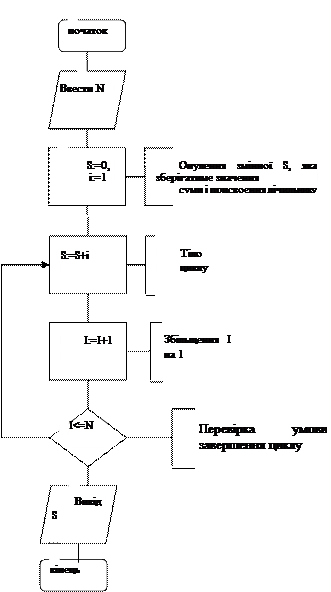Приклад: Обчислити суму перших N натуральних чисел.
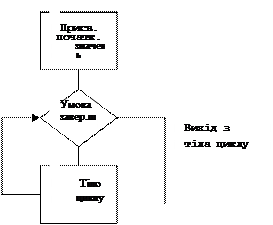Цикли з невідомим числом повторень.
В циклах з невідомим числом повторень умова виходу з циклу перевіряється перед виконанням операторів тіла циклу. При використанні циклів з невідомим числом повторень (ітераційні цикли) необхідно в тілі циклу змінювати значення змінних, що входять в умову завершення циклу.
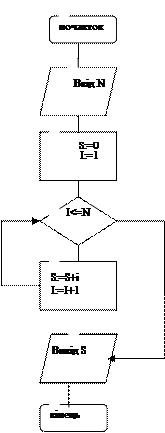
Попередній приклад можна реалізувати і з допомогою циклу з невідомим числом повторень.
Обчислення сум та добутків.
Задача обчислення сум та добутків дуже часто зустрічається при побудові алгоритмів. Ми вже розглянули приклад накопичення суми перших N натуральних чиcел. Характерною ознакою цього алгоритму є присвоєння змінній, якою ми позначаємо суму, нульового початкового значення. При обчисленні добутків, змінній, якою позначатимемо добуток, необхідно очевидно присвоїти початкове значення 1.
ПРИКЛАД: Згідно з означенням, факторіалом натурального числа N
називаєтьоя добуток всіх натуральних чисел, які не перевищують N, тобто
N! = 1 * 2 * 3 * …*(N-і) * N, при цьому 0! приймаотьоя рівним 1.
Складемо блок-охему алгоритму обчиолення N!
