Редактор Н.В. Городник
Технический редактор Н.В. Белова
Компьютерная верстка Г.И. Якименко
_____________________________________________________________________
Подписано в печать 03.07.2006. Формат 60 х 84 1/16. Бумага офсетная
Тираж 200 экз. Уч.-изд. л. 1,39. Печ. л. 1,5. Изд. № 69
Заказ № Цена договорная
_____________________________________________________________________
Отпечатано в типографии
Новосибирского государственного технического университета
 630092, г. Новосибирск, пр. К. Маркса, 20
630092, г. Новосибирск, пр. К. Маркса, 20
Кафедра прикладної математики
Тексти лекцій
Та завдання до лабораторних робіт
з курсу “Програмування та алгоритмічні мови”
семестр
Львів-2003
1. Задання алгоритму
Поняття алгоритму.
Алгоритм — це конструктивно задане правило (закон), за яким вхідній інформації (умовам задачі) ставиться у відповідність нова вихідна інформація (розв'язок задачі). Інакше кажучи, алгоритм — це деякий скінченний набір операцій, виконання яких одна за однією через скінченне число кроків приводить до поставленої мети (розв'язку задачі). Поняття алгоритму належить до базових понять і не означається через простіші поняття.
Алгоритм повинен володіти властивостями:
1. Масовість Алгоритм повинен бути застосовним до широкого класу задач.
2. Визначеність (детермінованість). Описання множини операцій, якою визначається алгоритм, не повинні допускати двояких тлумачень. При виконанні операцій не повинно виникати питань, що саме і як треба робити. Строго визначеним повинен бути і порядок виконання операцій.
3. Дискретність. Процес, який визначається алгоритмом, повинен мати дискретний (перервний) характер, тобто являти собою послідовність окремих завершених кроків. Кожна операція алгоритму повинна виконуватися за скінченний час, а виконання наступної операції повинно починатися після завершення попередньої.
4. Результативність. Виконання послідовності операцій, якою визначається алгоритм, через скінченне, можливо досить значне, число кроків приводить до цілком певного результату Виконання алгоритму не може закінчуватися невизначеною ситуацією або ж зовсім не закінчуватися.
Кожен алгоритм передбачає наявність деяких вхідних даних і його виконання за скінченний час приводить до цілком певних результатів.
5. Формальність. Будь-який виконавець, здатний сприймати і виконуючи вказівки алгоритму, виконає поставлене завдання.
6. Захищеність. Алгоритм повинен бути захищеним від несанкціонованого використання (використання без дозволу авторів) та некваліфікованого користувача (некоректне задання початкових даних).
7. Дружелюбність. Алгоритим завжди готовий вказати виконавцю на його помилки.
Набір операцій, виконанню яких навчено виконавця і які можуть бути включені у множину операцій, якою визначається алгоритм, називають системою операцій (вказівок) виконавця. Може трапитися, що множина допустимих операцій виявиться такою, що в результаті виконання будь-якої скінченної послідовності операцій не вдасться виконати поставлене завдання. Надалі вважатимемо, що виконавець має достатню для виконання поставленого перед ним завдання множину допустимих операцій.
Якщо виконавця навчено виконувати вказану операцію, тобто вказівка про виконання завдання входить до системи допустимих для нього вказівок, то описання алгоритму складається з однієї вказівки, тобто множина операцій, якою визначається алгоритм, містить єдину операцію.
Якщо ж виконавця не навчено виконувати поставлене завдання, то виникає потреба вказану операцію розкласти на деяку сукупність простіших операцій. Якщо всі такі операції входять до системи операцій виконавця, то описання алгоритму на цьому закінчується. Якщо ж серед вказаних операцій є такі, що не входять до системи операцій виконавця, то такі операції розкладаються на сукупність ще простіших операцій. Таке розкладання операцій на простіші продовжується доти, поки утвориться сукупність операцій, кожна з яких входить до системи операцій виконавця. Такий метод конструювання алгоритмів називають методом покрокової деталізації зверху вниз. Існують різні форми задання алгоритмів: словесні, словесно-формульні, графічні, у вигляді послідовності кодів з деякого скінченного набору кодів та інші — залежно від того, на якого виконавця орієнтовано алгоритм. При складанні алгоритмів часто поєднують різні форми.
Зображення алгоритму у вигляді блок-схеми.
Блок-схемою називається графічне зображення алгоритму, при якому окремі кроки (етапи) алгоритму зображаються з допомогою геометричних фігур (символів), а зв’язки між етапами задаються з допомогою ліній потоків, що з’єднують символи.
Символ ПРОЦЕС зображається у вигляді прямокутника з відношенням сторін a:b =2:3, де a вибирається з множини { 10, 15, 20, 50, 75, 100 мм.}. Необхідно відмітити, що всі наступні символи вписуватимуться у задані розміри. Інформація про перетворення, які виконує символ, записуються всередині символа.
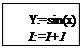 Приклад. Змінній Y присвоюється значення sin(x) і значеннязмінної i збільшується на 1.
Приклад. Змінній Y присвоюється значення sin(x) і значеннязмінної i збільшується на 1.
 Символ РОЗГАЛУЖЕННЯ зображається у вигляді ромба, діагоналі якого рівні a та b. Цей символ має один вхід і два виходи, кожен з яких у залежності від виконання умови, позначається “так” або “ні” і задає напрям продовження обчислень. Ми відмітили стрілочками напрями потоків, які входять у символ розгалуження і виходять з нього. У майбутньому лінії потоків, що йдуть зверху-вниз та зліва-направо, вважатимемо природніми і стрілочками не позначатимемо.
Символ РОЗГАЛУЖЕННЯ зображається у вигляді ромба, діагоналі якого рівні a та b. Цей символ має один вхід і два виходи, кожен з яких у залежності від виконання умови, позначається “так” або “ні” і задає напрям продовження обчислень. Ми відмітили стрілочками напрями потоків, які входять у символ розгалуження і виходять з нього. У майбутньому лінії потоків, що йдуть зверху-вниз та зліва-направо, вважатимемо природніми і стрілочками не позначатимемо.
 Символ ПОЧАТОК-КІНЕЦЬ обчислень зображається графічно як прямокутник з заокругленими кінцями і висотою a/2 та служить для задання початку і кінця алгоритму.
Символ ПОЧАТОК-КІНЕЦЬ обчислень зображається графічно як прямокутник з заокругленими кінцями і висотою a/2 та служить для задання початку і кінця алгоритму.
Небхідно пам’ятати, що лінії потоків йдуть паралельно зовнішньому краю блок-схеми, тобто строго вертикально і горизонтально.
 Етапи ВВОДУ-ВИВОДУ відображаються при допомозі символа паралелограма.
Етапи ВВОДУ-ВИВОДУ відображаються при допомозі символа паралелограма.
 У ряді випадків не всю інформацію про перетворення, які виконує символ, можна у ньому розмістити; хоча б з огляду на те, що символ чисто фізично займає обмежену площу. У таких випадках, інформацію про перетворення, які виконує символ, виносять за межі символа. Вся інформація записується після відкритої квадратної дужки, з'єднаної з символом лінією потоку.
У ряді випадків не всю інформацію про перетворення, які виконує символ, можна у ньому розмістити; хоча б з огляду на те, що символ чисто фізично займає обмежену площу. У таких випадках, інформацію про перетворення, які виконує символ, виносять за межі символа. Вся інформація записується після відкритої квадратної дужки, з'єднаної з символом лінією потоку.
ПРИКЛАД: При такому запиcі (декілька перетворень в одному оимволі), порядок їхнього виконання відповідає порядку запису.
Для полегшення аналізу алгоритму та підвищення його читабельності бажано документувати ( коментувати ) дії, які виконує символ. Коментарі записуються у довільній формі після відкритої квадратної дужки, з'єднаної з символом пунктирною лінією.
 ПРИКЛАД:
ПРИКЛАД:
ПРИКЛАД. Розглянемо довільне ціле чиcло N. Як перевірити, чи задане число є парним і двоцифровим. Цю задачу можна розбити на дві підзадачі:
а) перевірити, чи N - парне;
б) перевірити, чи N - двоцифрове.
При реалізації алгоритмів ми вже використовували математичні функції (sinx. cosх. lnх, ex і т.п. ). Для реалізацїї нашого завдання у вигляді алгоритму скориcтаємось функцією entier(х), яка виділяє цілу чаcтину аргумента х, для прикладу: entier(5.7)=5, entier(-4.2)=-4. Тоді для перевірки парності числа N можна запиcати умову, 2*entier(N/2)= N, а entier(N/10), якщо N - двоцифрове чиcло, задає кількість десятків у ньому. Дійсно, нескладно перевірити, що при N = 25, entier(25/10)=2.


 Поняття про структурний підхід
Поняття про структурний підхід


 630092, г. Новосибирск, пр. К. Маркса, 20
630092, г. Новосибирск, пр. К. Маркса, 20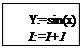 Приклад. Змінній Y присвоюється значення sin(x) і значеннязмінної i збільшується на 1.
Приклад. Змінній Y присвоюється значення sin(x) і значеннязмінної i збільшується на 1. Символ РОЗГАЛУЖЕННЯ зображається у вигляді ромба, діагоналі якого рівні a та b. Цей символ має один вхід і два виходи, кожен з яких у залежності від виконання умови, позначається “так” або “ні” і задає напрям продовження обчислень. Ми відмітили стрілочками напрями потоків, які входять у символ розгалуження і виходять з нього. У майбутньому лінії потоків, що йдуть зверху-вниз та зліва-направо, вважатимемо природніми і стрілочками не позначатимемо.
Символ РОЗГАЛУЖЕННЯ зображається у вигляді ромба, діагоналі якого рівні a та b. Цей символ має один вхід і два виходи, кожен з яких у залежності від виконання умови, позначається “так” або “ні” і задає напрям продовження обчислень. Ми відмітили стрілочками напрями потоків, які входять у символ розгалуження і виходять з нього. У майбутньому лінії потоків, що йдуть зверху-вниз та зліва-направо, вважатимемо природніми і стрілочками не позначатимемо. Символ ПОЧАТОК-КІНЕЦЬ обчислень зображається графічно як прямокутник з заокругленими кінцями і висотою a/2 та служить для задання початку і кінця алгоритму.
Символ ПОЧАТОК-КІНЕЦЬ обчислень зображається графічно як прямокутник з заокругленими кінцями і висотою a/2 та служить для задання початку і кінця алгоритму. Етапи ВВОДУ-ВИВОДУ відображаються при допомозі символа паралелограма.
Етапи ВВОДУ-ВИВОДУ відображаються при допомозі символа паралелограма. У ряді випадків не всю інформацію про перетворення, які виконує символ, можна у ньому розмістити; хоча б з огляду на те, що символ чисто фізично займає обмежену площу. У таких випадках, інформацію про перетворення, які виконує символ, виносять за межі символа. Вся інформація записується після відкритої квадратної дужки, з'єднаної з символом лінією потоку.
У ряді випадків не всю інформацію про перетворення, які виконує символ, можна у ньому розмістити; хоча б з огляду на те, що символ чисто фізично займає обмежену площу. У таких випадках, інформацію про перетворення, які виконує символ, виносять за межі символа. Вся інформація записується після відкритої квадратної дужки, з'єднаної з символом лінією потоку. ПРИКЛАД:
ПРИКЛАД:
