1 Є n міст, зв'язаних мережею шосейних доріг. Відома відстань між містами, якщо вони зв'язані дорогою. Необхідно знайти найкоротший шлях і його довжину від вказаного міста відправлення до будь-якого іншого відомого міста (метод Форда визначення найкоротшого шляху на графі в інтерпретації Дейкстри). Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Дискретна математика”.
2 Є n міст, зв'язаних мережею шосейних доріг. Відома відстань між містами, якщо вони зв'язані дорогою. Необхідно знайти довжини найкоротших шляхів між будь-якими двома відомими містами (метод Шимбела визначення найкоротшого шляху на графі ). Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Дискретна математика”.
3 “Життя” – це багатоклітинна істота, яка населяє прямокутну пустелю. Пустеля розбита на осередки, подібні до клітин шахівниці. Осередок|чарунка,вічко,комірка| може бути порожнім|пустим| або вміщати одну клітинку життя. У цьому світі “життя” розвивається за кроками. За один крок в одних осередках клітини гинуть, а в інших- зароджуються. Зміна поколінь “життя” відбувається за такими правилами:
- сусідами клітини називаються клітини, що знаходяться у восьми осередках, дотичних з осередком, що містить клітину;
- якщо клітина має двох або трьох сусідів, то вона зберігає себе на наступному такті “життя”;
- якщо клітина має більше ніж три або менше ніж два сусіди – вона гине. У першому випадку – від перенаселеності, у другому – від “самотності”;
- якщо у клітині немає “життя”, але у неї рівно три сусідні клітини, то у ній зароджується “життя”.
Необхідно написати програму, що дозволяє визначати стан “життя” через вказану кількість кроків. Питання про розміри пустелі та її заповнення вирішити самостійно.
4 Існує n груп 2-го і 3-го курсів, які необхідно розподілити в n комп'ютерних класів для проведення лабораторних занять. На підставі наявних статистичних досліджень визначено продуктивність кожної групи у кожному комп'ютерному класі. Необхідно так розподілити групи по класах, щоб сумарна продуктивність на заняттях з програмування була максимальною (угорський метод розв’язанн задачі вибору: виконати крок приведення масиву і вибір незалежних нулів). Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліні “Методи оптимізації”.
5 Умова завдання №4:
- реалізувати крок пошуку мінімального покриття матриці і її наступного приведення.
6 Задана “s/t - мережа”, яка складається з n міст і m дуг. Необхідно визначити величину максимального потоку в “s/t - мережі” (теорема Форда - Фалкерсона). Теоретичний матеріал див. у методичних вказівках до виконання семестрової роботи з дисципліни “Дискретна математика”.
7 Транспортна задача: вибір початкового опорного розв'язання методом північно-західного кута. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.
8 Транспортна задача: вибір початкового опорного розв'язання методом мінімального елемента. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”
9 Транспортна задача: вибір початкового опорного розв'язання методом Фогеля. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.
10 Транспортне задача: покращання опорного плану методом потенціалів. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.
11 Симплексний метод розв'язання ЗЛП: побудова симплексної таблиці, вибір розв’язувального елемента. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.
12 Симплексний метод розв'язання ЗЛП: перерахунок симплексної таблиці, визначення оптимальності одержаного розв’язку . Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Методи оптимізації”.
13 Задано три послідовності: U(розмірності n), X(розмірності m), Y(розмірності r). Ураховуючи, що послідовність U – універсальна множина, послідовності X і Y – підмножини універсальної множини, необхідно знайти:
- об'єднання множин X і Y;
- перетин множин X і Y;
- різниця множин X і Y, Y і X;
- доповнення множин X і Y;
- прямий добуток множин X і Y.
Передбачити можливість некоректного завдання множин U, X, Y. Теоретичний матеріал див. у методичних вказівках щодо виконання семестрової роботи з дисципліни “Дискретна математика”.
14 Задано дві матриці А={aij} розмірності n´n і B={bij} розмірності m´g. Для кожної з них поміняти місцями другий і третій стовпці та елементи рядка, який містить найбільший елемент матриці, замінити нулями. Підрахувати значення найбільшого мінора для матриць А і В.
15 Скласти функцію для підрахунку елементів матриці С={cij}, розмірності m´ g, що являється добутком матриць А={aij} розмірності m´ n і B={bij} розмірності n´ g. У масиві В поміняти місцями рядки, які вибирає користувач.
16 Скласти функцію для обчислення елементів матриці С={cij}, яка є сумою матриць А={aij} і B={bij} розмірності n ´ n. Причому матриця А може бути задана довільно, а елементи матриці B визначаються наступним чином: 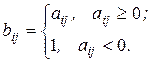
Потім у матриці А замінити всі від’ємні елементи найменшим у кожному рядку відповідно, а додатні- замінити залишком від ділення елемента на 2.
17 Скласти функцію для обчислення|підрахунку| вектора Z={zi}, i=1..m, що дорівнює добутку матриці А={aij} розмірності m ´ n на вектор Х={хj}, елементи якого обчислюють за формулою 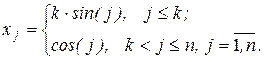 Перевірити, чи являються елементи вектора Z упорядкованими за зменшенням. Якщо ні, то показати перший елемент, що порушив порядок зменшування, а також номер цього елемента, виправити порушення, тобто розташувати елементи у порядку зменшування.
Перевірити, чи являються елементи вектора Z упорядкованими за зменшенням. Якщо ні, то показати перший елемент, що порушив порядок зменшування, а також номер цього елемента, виправити порушення, тобто розташувати елементи у порядку зменшування.
18 Скласти функцію, яка у заданій матриці А розмірності m´n знаходить число R - найменше з позитивних відношень, де s – номер стовпця, у якому елемент ais є негативним. У масиві А замінити елементи стовпця знайменшим значенням нулями.
19 Написати програму, яка будує матрицю А розмірності n´n з компонентами, визначуваними за формулою: aij= sin(i+j)××x, i,j=1..n, x – довільна дійсна величина. Потім у кожному рядку А замінити найбільший елемент абсолютною величиною діагонального елемента, а від’ємні елементи замінити їх кубами. Далі розташувати елементи кожного рядка у порядку зростання.
20 У масиві А={aij} розмірності n ´ n знайти різницю між сумою і добутком елементів масиву. Потім у кожному рядку знайти найбільший елемент і впорядкувати всі елементи у правильному порядку відносно до найбільшого, тобто якщо існує рядок {1.2; 0.5; 7.0; 2.6; 5.0}, то після впорядкування має вийти рядок {0.5; 1.2; 7.0; 5.0; 2.6}.
21 Скласти функцію для обчислення матриці B={bij}, яка є добутком числа g на матрицю А={aij} розмірності n ´ n. Число g – найбільший елемент заданого вектора Z. Потім у матриці В замінити діагональні елементи найбільшими елементами кожного стовпця відповідно.
22 Скласти функцію для обчислення вектора B={bi}, що дорівнює тому рядку матриці А={aij} розмірності n ´ n, у якій розташовано найбільший елемент матриці, та вектора С={ci}, який є таким стовпцем матриці А, у якому знаходиться найменший елемент матриці. Потім упорядкувати елементи знайдених векторів у порядку зростання елементів.
23 Задано дві матриці А={aij} розмірності n´n і B={bij} розмірності m´g. Для кожної з них визначити добуток від’ємних елементів і їх кількість. Упорядкувати елементи рядків у матриці А і стовпців матриці В у порядку зростання лінійним швидким сортуванням.
24 Задано матрицю А={aij} розмірності m´n. Скласти функцію для побудови логічного вектора B={bi} за наступним правилом: якщо у рядку з номером k кількість додатних елементів більша ніж кількість від’ємних, то bk=1(true), інакше bk=0(false). Потім необхідно розташувати елементи кожного стовпця масиву А у порядку зменшення лінійним сортуванням.
25 Задано матрицю А={aij} розмірності n´n. Скласти функцію для побудови вектора B={bi} за наступним правилом: якщо aii<0, то bi узяти таким, що дорівнює сумі елементів і - го рядка, інакше – суму абсолютних величин і - го стовпця. Потім у матриці А розташувати елементи кожного рядка у порядку зростання.
26 Уведено матрицю А={aij} розмірності m´n. Скласти функцію для побудови|шикування| логічного вектора B={bi} за наступним|слідуючим| правилом: якщо і - ий рядок матриці А утворює незбутню послідовність, то bk=1(true), інакше bk=0(false). Потім у матриці А для кожного рядка визначити номери найменших елементів і добуток елементів, що йдуть за ними.
27 Уведено логічний вектор А={ai} і дійсний Х={хi} і=1.. n. Скласти функцію для перетворення вектора Х за правилом: якщо ai=1(true), то хi помножити на 10, інакше – розділити на -10. Потім у векторі Х замінити додатні елементи найбільшим серед додатних, а від’ємні – найменшим серед від’ємних.
28 Написати аналог гри “Хрестики - нулі”.
29 Задано куб 2´2´2, грані якого розбито на чотири однакові сектори 1´1. Кожний з секторів розфарбовано довільним чином. Визначити, чи розфарбовано кожну з граней куба одним кольором. Спосіб зберігання даних визначити самостійно.
30 Задано масив 3´3, заповнений довільно числами від 1 до 8, одна комірка масиву “умовно порожня”. Використовуючи принцип гри у квача, упорядкувати елементи масиву.


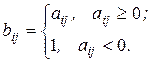
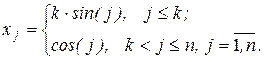 Перевірити, чи являються елементи вектора Z упорядкованими за зменшенням. Якщо ні, то показати перший елемент, що порушив порядок зменшування, а також номер цього елемента, виправити порушення, тобто розташувати елементи у порядку зменшування.
Перевірити, чи являються елементи вектора Z упорядкованими за зменшенням. Якщо ні, то показати перший елемент, що порушив порядок зменшування, а також номер цього елемента, виправити порушення, тобто розташувати елементи у порядку зменшування.