Приклад використання масивів для збереження та оброблення однотипових даних.
Нехай задано деяку квадратну матрицю розмірності n ´ n, яка містить дійсні числа. Розіб’ємо дану матрицю на чотири сектори однакового розміру, як показано на рис.1. Будемо вважати, що квадратна матриця є збалансованою,
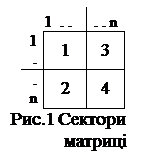 якщо сума елементів першого та четвертого секторів дорівнює сумі елементів другого та третього секторів. Необхідно написати програму, яка б для будь – якої матриці заданого розміру визначала, чи є така матриця збалансованою.
якщо сума елементів першого та четвертого секторів дорівнює сумі елементів другого та третього секторів. Необхідно написати програму, яка б для будь – якої матриці заданого розміру визначала, чи є така матриця збалансованою.
Для збереження елементів матриці використаємо статичний двовимірний масив даних типу float, а для підрахунку необхідних сум – статичний одномірний масив даних типу float, елементи якого спочатку завжди дорівнюватимуть нулю:
float mas[10][10]; ],//оголошення масиву mas, який містить 100 елементів типу;
float Sum[]={0,0,0,0};//оголошення масиву Sum з чотирма елементами, які //дорівнюють нулю;
int i,j,n;
cin>>n; //ввід кількості елементів масиву
for(i=0;i<n;i++)
for(j=0;j<n;j++)
cin>>mas[i][j]; // внесення значень елементів масиву.
Для визначення суми елементів за секторами необхідно спочатку визначити розмір сектора. Для цього достатньо виконати наступну дію:
int rozmir=n/2;
У даному випадку використане ціле ділення. Тобто, якщо n є числом, яке не кратне 2, змінна rozmir буде цілим числом. Це дозволяє відкинути середній стовпчик і рядок під час визначення розміру сектора, якщо n є числом, яке не кратне 2.
Обчислення суми елементів в секторах можна проводити окремо з кожному сектора, але це збільшить загальний час виконання програми, тому підрахунок сум виконаємо одночасно за один прохід циклу. Наведений нижче фрагмент програми демонструє використання циклів для проходу по всіх елементах масиву і підрахунку всіх чотирьох сум:
for(i=0;i<centr;i++)
for(j=0;j<centr;j++)
{ Sum[0]+=mas[i][j]; //підрахунок суми у першому секторі
Sum[1]+=mas[n-1-i][j]; //підрахунок суми у другому секторі
Sum[2]+=mas[i][n-1-j]; //підрахунок суми у третьому секторі
Sum[3]+=mas[n-1-i][n-1-j]; //підрахунок суми у четвертому секторі
}
Підрахунок суми елементів першого та третього секторів проводить, починаючи з елементів рядка з нульовим індексом у прямому напрямку, другого і четвертого секторів – починаючи з останнього елемента рядка у зворотному напрямку. Аналогічно, накопичення суми елементів першого та другого секторів проводать, починаючи з нульового елемента стовпчика у прямому напрямку, для третього та четвертого секторів – починаючи з останнього елемента стовпчика у зворотному напрямку.
Таким чином, у цілому програма визначення збалансованості заданої матриці матиме вигляд:
#include <iostream.h>
#include <conio.h>
void main()
{ float mas[10][10];
float Sum[]={0,0,0,0};
int i,j,n;
cin>>n;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
cin>>mas[i][j];
int rozmir=n/2;
cout<<"\nc="<<centr+n%2;
for(i=0;i<rozmir;i++)
for(j=0;j<rozmir;j++)
{Sum[0]+=mas[i][j];
Sum[1]+=mas[n-1-i][j];
Sum[2]+=mas[i][n-1-j];
Sum[3]+=mas[n-1-i][n-1-j];
}
for(i=0;i<4;i++)
cout<<"\nSum["<<i<<"]="<<Sum[i];
if ((Sum[0]==Sum[3])&&(Sum[1]==Sum[2])) cout<<"\n збалансована";
else cout<<"\n не збалансована";
getch();}
Зміст|вміст,утримання| звіту щодо лабораторної роботи №3
1. Титульна сторінка |аркуш|: назва дисципліни; номер і найменування роботи; прізвище, ім'я, по батькові студента; дата виконання.
2. Поставлення завдання|задачі|. Слід дати конкретне поставлення, тобто вказати, який масив даних потрібно створити, які під задачі мають розв’язувати.
3. Математична схема розв’язання поставленої задачі
4. Визначення основних змінних і функцій з|із| коментарями.
5. Реалізація функцій.
6. Лістинг основної програми, де має бути вказано, в якому місці та яка функція викликається|спричиняються|.


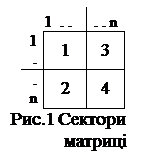 якщо сума елементів першого та четвертого секторів дорівнює сумі елементів другого та третього секторів. Необхідно написати програму, яка б для будь – якої матриці заданого розміру визначала, чи є така матриця збалансованою.
якщо сума елементів першого та четвертого секторів дорівнює сумі елементів другого та третього секторів. Необхідно написати програму, яка б для будь – якої матриці заданого розміру визначала, чи є така матриця збалансованою.