ІІ ітерація

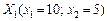Узявши точку , обчислюємо значення градієнта в ній: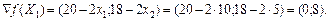

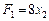Використовуючи розраховане значення градієнта, вводимо нову цільову функцію: . Отримуємо таку задачу лінійного програмування: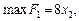

.

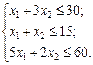
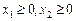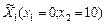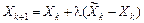Розв’язавши її симплексним методом, отримуємо оптимальний план: .

За формулою визначаємо координати наступної точки наближення.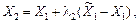

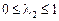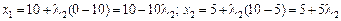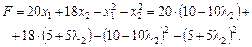
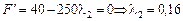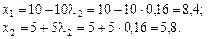
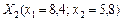Визначаємо координати точки Х₂:

,

.

Знайдемо такий крок λ₂, за якого досягається максимальне значення цільової функції:

Матимемо .

Обчислимо координати наступної точки Х₂:

Для знайденої точки значення цільової функ­ції дорівнює: .

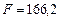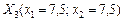Продовжуючи процес у аналогічний спосіб, на ІІІ ітерації визначаємо точку і переконуємося, що значення цільової функції знову зростає: .

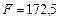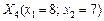На IV ітерації розраховуються координати точки , для якої .

V ітерація

Узявши точку , обчислюємо значення градієнта в ній:

.

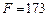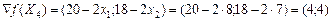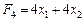Використовуючи значення цього вектора (градієнта), вводимо нову цільову функцію: і маємо таку задачу лінійного програмування:

,

.

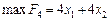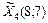Розв’язавши цю задачу, отримаємо значення оптимального плану , тобто повертаємося до попереднього значення. Отже, точку з координатами 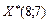вважаємо оптимальним планом, оскільки маємо нульовий градієнт функції, тобто цей план поліпшити вже не можна.