Розглянемо тепер задачу (1) – (2) , якщо на змінні 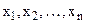 накладаються умови обмежень у вигляді рівностей:
накладаються умови обмежень у вигляді рівностей:
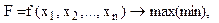 ( 12 )
( 12 )
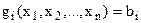 ,
, 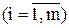 , ( 13 )
, ( 13 )
де функції 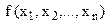 і
і 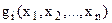 двічі неперервно диференційовані функції.
двічі неперервно диференційовані функції.
У курсі математичного аналізу задача (12) – (13) називається задачею на умовний екстремум або класичною задачею оптимізації. Умова (13) називається рівнянням зв’язку. Для розв’язання такої задачі використовується метод множників Лагранжа.
Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення дальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних.
Для знаходження розв’язку задачі (12) – (13) замінимо цільову функцію (13) на іншу. Ця функція називається функцією Лагранжа і має такий вигляд:
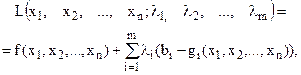 (14)
(14)
де 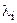 — деякі невідомі величини, що називаються множниками Лагранжа.
— деякі невідомі величини, що називаються множниками Лагранжа.
Тоді відшукання умовного екстремуму задачі (12) – (13) зводиться до знаходження безумовного екстремуму функції Лагранжа (14). Знайдемо частинні похідні цієї функції і прирівняємо їх до нуля:
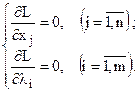
або 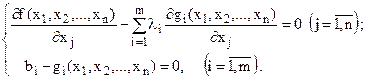 (15)
(15)
Друга група рівнянь системи (15) забезпечує виконання умов (13) початкової задачі нелінійного програмування.
Система (15), як правило, нелінійна. Розв’язками її є 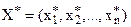 і
і 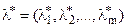 — стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (12), (13) або можуть бути точками перегину (сідловими точками).
— стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (12), (13) або можуть бути точками перегину (сідловими точками).
Для діагностування стаціонарних точок і визначення типу екстремуму необхідно перевірити виконання достатніх умов екстремуму, тобто дослідити в околі стаціонарних точок диференціали другого порядку (якщо для функцій 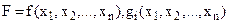 існують другі частинні похідні і вони неперервні). Перевірка виконання достатніх умов екстремуму виконується так само, як і у розглянутому вище випадку безумовного екстремуму.
існують другі частинні похідні і вони неперервні). Перевірка виконання достатніх умов екстремуму виконується так само, як і у розглянутому вище випадку безумовного екстремуму.
6. Опукле програмування
Найбільш вивченими і обґрунтованими задачами є задачі опуклого програмування, тобто задачі математичного програмування, в яких цільова функція є опуклою (або вгнутою), а область допустимих розв’язків – опуклою множиною. Перевагою задач опуклого програмування є те що цільова функція завжди має екстремум, причому глобальний.
Означення 1. Функція 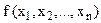 ,що задана на опуклій множині
,що задана на опуклій множині 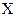 , називається опуклою, якщо для будь-яких двох точок
, називається опуклою, якщо для будь-яких двох точок 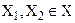 і довільного
і довільного 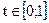 виконується співвідношення
виконується співвідношення
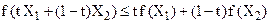 .
.
Означення 2. Функція 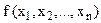 ,що задана на опуклій множині
,що задана на опуклій множині 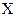 , називається вгнутою, якщо для будь-яких двох точок
, називається вгнутою, якщо для будь-яких двох точок 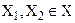 і довільного
і довільного 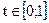 виконується співвідношення
виконується співвідношення
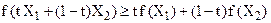 .
.
Якщо функція 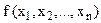 - опукла,тофункція
- опукла,тофункція 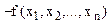 - вгнута.
- вгнута.
Загальна постановка задачі опуклого програмування має вигляд:
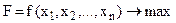 , (16)
, (16)
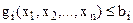 ,
, 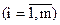 , (17)
, (17)
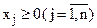 , (18)
, (18)
де 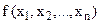 - вгнута, а
- вгнута, а 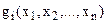 — опуклі функції. Якщо задача опуклого програмування задається на мінімум, то функція
— опуклі функції. Якщо задача опуклого програмування задається на мінімум, то функція 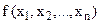 мусить бути опуклою.
мусить бути опуклою.
Множина допустимих планів задачі, що визначається системою (17), є опуклою. Будемо вважати надалі, що область допустимих розв’язків (17) – (18) задачі (16) – (18) не порожня і обмежена.
Терема 1. Довільний локальний максимум (мінімум) задачі опуклого програмування є глобальним максимумом (мінімумом).
Отже, якщо визначено точку локального екстремуму задачі опуклого програмування, то це означає, що знайдено точку глобального максимуму (мінімуму).
Означення 3.Множина допустимих планів (17) – (18) задовольняє умову регулярності, якщо існує хоча б одна точка 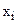 з області допустимих планів така, що
з області допустимих планів така, що 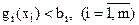 .
.
У разі обмежень-нерівностей задачу опуклого програмування розв’язують, застосовуючи метод множників Лагранжа. Функція Лагранжа для задачі (16)—(18) має вид:
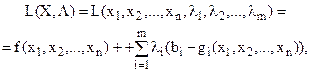 (19)
(19)
де 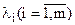 — множники Лагранжа.
— множники Лагранжа.
Означення4. Точка 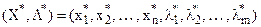 називається сідловою точкою функції Лагранжа якщо
називається сідловою точкою функції Лагранжа якщо 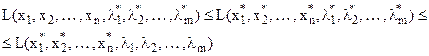
для всіх 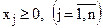 і
і 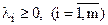 .
.
Теорема 2. (теорема Куна-Таккера).Нехай для області допустимих розв’язків задачі опуклого програмування (16) – (18) виконується умова регулярності. План 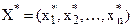 буде оптимальним планом цієї задачі тоді і тільки тоді, коли існує такий вектор
буде оптимальним планом цієї задачі тоді і тільки тоді, коли існує такий вектор 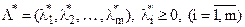 , що пара
, що пара 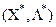 - сідлова точка функції Лагранжа.
- сідлова точка функції Лагранжа.
Використовуючи теорему Куна — Таккера, маємо необхідні та достатні умови існування оптимального плану задачі опуклого програмування:
(І) 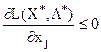 ,
, 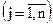 ; (20)
; (20)
(ІІ) 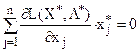 ,
, 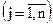 ; (21)
; (21)
(ІІІ) 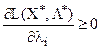 ,
,  ; (22)
; (22)
(IV) 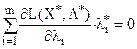 ,
,  . (23)
. (23)
Для задачі мінімізації,де всі функції 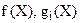
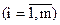 диференційовні і опуклі по Х, маємо умови, аналогічні вищенаведеним, але зі знаком «≥» в нерівностях (21) та (23).
диференційовні і опуклі по Х, маємо умови, аналогічні вищенаведеним, але зі знаком «≥» в нерівностях (21) та (23).
Зауваження 1. Теорему Куна – Танкера можна розглядати як узагальнення теореми двоїстості у лінійному програмуванні, а множники Лагранжа – як двоїсті оцінки.
Зауваження 2. Умови Куна – Танкера мало придатні для знаходження оптимального розв’язку, вони лише характеризують розв’язок, тобто дають можливість перевірити деякий розв’язок на оптимальність.
Розглянемо тепер задачу квадратичного програмування, яка є окремим випадком задачі опуклого програмування. Специфіка цієї задачі полягає утому, що система обмежень є лінійною, а цільова функція квадратичною.
Означення 5. Квадратичною формою відносно змінних 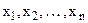 називається числова функція від цих невідомих вигляду
називається числова функція від цих невідомих вигляду
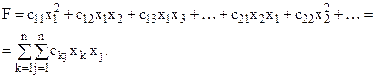
Означення 6. Квадратична форма 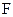 називається додатньо (від’ємно) – визначеною, якщо
називається додатньо (від’ємно) – визначеною, якщо 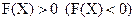 для усіх значень змінних
для усіх значень змінних 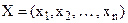 , окрім
, окрім  .
.
Означення 7. Квадратична форма 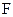 називається додатньо (від’ємно) – напіввизначеною, якщо
називається додатньо (від’ємно) – напіввизначеною, якщо 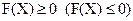 для будь-якого набору значень змінних
для будь-якого набору значень змінних 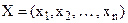 і, крім того існує такий набір змінних
і, крім того існує такий набір змінних 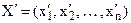 , де не всі значення змінних одночасно дорівнюють нулю, так що
, де не всі значення змінних одночасно дорівнюють нулю, так що 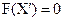 .
.
Теорема 3.Квадратичнаформа є опуклою функцією, якщо вона додатньо-напіввизначена, і є вгнутою функцією, якщо вона від’ємно-напіввизначена.
Постановка задачі квадратичного програмування має вигляд:
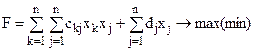 ,( 24 )
,( 24 )
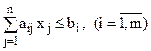 ,( 25 )
,( 25 )
 , ( 26 )
, ( 26 )
де 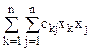 -від’ємно(додатньо) – напіввизначена квадратична форма.
-від’ємно(додатньо) – напіввизначена квадратична форма.
Функція Лагранжа для сформульованої задачі квадратичного програмування запишеться у вигляді:
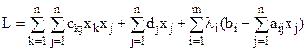 .
.
Якщо функція Лагранжа 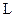 має сідлову точку
має сідлову точку 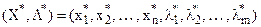 ,то в цій точці виконуються співвідношення (20) – (23). Ввівши тепер додаткові змінні
,то в цій точці виконуються співвідношення (20) – (23). Ввівши тепер додаткові змінні 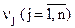 і
і 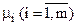 , що перетворюють нерівності (20) і (22) у рівності, перепишемо вирази (20) – (23) для задачі квадратичного програмування наступним чином:
, що перетворюють нерівності (20) і (22) у рівності, перепишемо вирази (20) – (23) для задачі квадратичного програмування наступним чином:
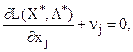
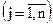 ,( 27 )
,( 27 )
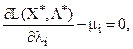
 ,( 28 )
,( 28 )

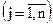 ,( 29 )
,( 29 )
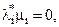
 ,( 30 )
,( 30 )
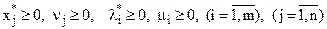 . ( 31 )
. ( 31 )
Щоб знайти розв’язок задачі квадратичного програмування (24) – (26), необхідно визначити невід’ємний розв’язок системи лінійних рівнянь (27) – (28), що задовольняє умовам (29) і (30). Цей розв’язок можна відшукати на основі методу штучного базису(М – методу). Через скінчене число кроків можна отримати або оптимальний план, або встановити нерозв’язність вихідної задачі.


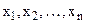 накладаються умови обмежень у вигляді рівностей:
накладаються умови обмежень у вигляді рівностей: 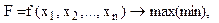 ( 12 )
( 12 )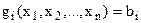 ,
, 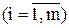 , ( 13 )
, ( 13 )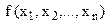 і
і 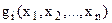 двічі неперервно диференційовані функції.
двічі неперервно диференційовані функції.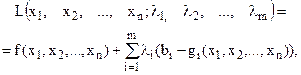 (14)
(14)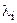 — деякі невідомі величини, що називаються множниками Лагранжа.
— деякі невідомі величини, що називаються множниками Лагранжа.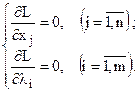
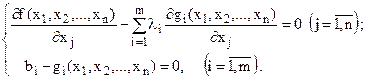 (15)
(15)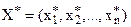 і
і 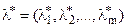 — стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (12), (13) або можуть бути точками перегину (сідловими точками).
— стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (12), (13) або можуть бути точками перегину (сідловими точками).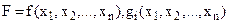 існують другі частинні похідні і вони неперервні). Перевірка виконання достатніх умов екстремуму виконується так само, як і у розглянутому вище випадку безумовного екстремуму.
існують другі частинні похідні і вони неперервні). Перевірка виконання достатніх умов екстремуму виконується так само, як і у розглянутому вище випадку безумовного екстремуму.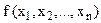 ,що задана на опуклій множині
,що задана на опуклій множині 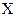 , називається опуклою, якщо для будь-яких двох точок
, називається опуклою, якщо для будь-яких двох точок 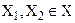 і довільного
і довільного 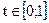 виконується співвідношення
виконується співвідношення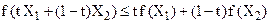 .
.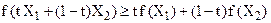 .
.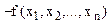 - вгнута.
- вгнута.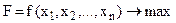 , (16)
, (16)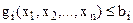 ,
, 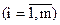 , (17)
, (17)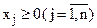 , (18)
, (18)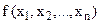 - вгнута, а
- вгнута, а 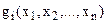 — опуклі функції. Якщо задача опуклого програмування задається на мінімум, то функція
— опуклі функції. Якщо задача опуклого програмування задається на мінімум, то функція 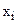 з області допустимих планів така, що
з області допустимих планів така, що 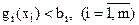 .
.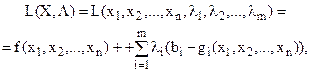 (19)
(19)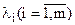 — множники Лагранжа.
— множники Лагранжа.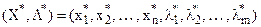 називається сідловою точкою функції Лагранжа якщо
називається сідловою точкою функції Лагранжа якщо 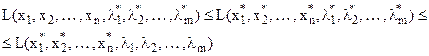
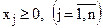 і
і 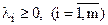 .
.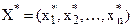 буде оптимальним планом цієї задачі тоді і тільки тоді, коли існує такий вектор
буде оптимальним планом цієї задачі тоді і тільки тоді, коли існує такий вектор 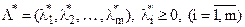 , що пара
, що пара 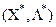 - сідлова точка функції Лагранжа.
- сідлова точка функції Лагранжа.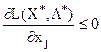 ,
, 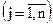 ; (20)
; (20)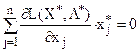 ,
, 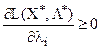 ,
,  ; (22)
; (22)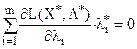 ,
, 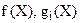
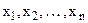 називається числова функція від цих невідомих вигляду
називається числова функція від цих невідомих вигляду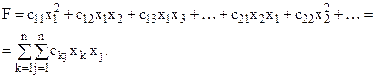
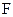 називається додатньо (від’ємно) – визначеною, якщо
називається додатньо (від’ємно) – визначеною, якщо 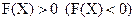 для усіх значень змінних
для усіх значень змінних 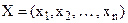 , окрім
, окрім  .
.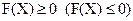 для будь-якого набору значень змінних
для будь-якого набору значень змінних 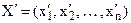 , де не всі значення змінних одночасно дорівнюють нулю, так що
, де не всі значення змінних одночасно дорівнюють нулю, так що 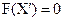 .
.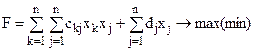 ,( 24 )
,( 24 )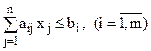 ,( 25 )
,( 25 ) , ( 26 )
, ( 26 )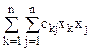 -від’ємно(додатньо) – напіввизначена квадратична форма.
-від’ємно(додатньо) – напіввизначена квадратична форма.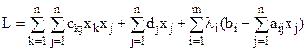 .
.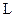 має сідлову точку
має сідлову точку 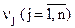 і
і 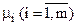 , що перетворюють нерівності (20) і (22) у рівності, перепишемо вирази (20) – (23) для задачі квадратичного програмування наступним чином:
, що перетворюють нерівності (20) і (22) у рівності, перепишемо вирази (20) – (23) для задачі квадратичного програмування наступним чином: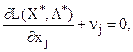
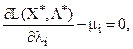

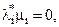
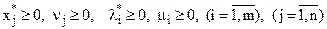 . ( 31 )
. ( 31 )